Let A,B,C,D,E represent vertices of a regular pentangon ABCDE. Given the position vector of these vertices be a,a+b,b,λa and λb respectively.
Q. AD divides EC in the ratio
cos2π5:1
cos3π5:1
1:2cos2π5
1:2
The correct Answer is:C
Given ABCDE is a regular pentagon

Let position vector of point A and C be →aandveb, respectively.
AD is parallel to BC and AB is parallel to EC.
Therefore,
AOCB is a parallelogram
and position vector of B is →a+→b
The position vectors of E and D are λ→bandλ→a respectively.
Also OA=BC=AB=OC=1 (let)
Therefore, AOCB is rhombus.
∠ABC=∠AOC=3π5
and ∠OAB=∠BCO=π−3π5=2π5
Further OA=AE=1andOC=CD=1
Thus, ΔEAOandΔOCD are isosceles.
In ΔOCD, using sine rule we get OCsin2π5=ODsinπ5
⇒OD=12cosπ5=OE
⇒AD=OA+OD=1+12cosπ2
⇒ADBC=1+12cosπ5=1+2cosπ52cosπ5
And OEOC=12cosπ5
Topper's Solved these Questions
- BOOK - CENGAGE ENGLISHCHAPTER - INTRODUCTION TO VECTORS EXERCISE - INTEGER TYPE8videos
INTRODUCTION TO VECTORS
- BOOK - CENGAGE ENGLISHCHAPTER - INTRODUCTION TO VECTORS EXERCISE - ARCHIVES SUBJECTIVE TYPE9videos
INTRODUCTION TO VECTORS
- BOOK - CENGAGE ENGLISHCHAPTER - INTRODUCTION TO VECTORS EXERCISE - REASONING TYPE11videos
INTRODUCTION TO VECTORS
- BOOK - CENGAGE ENGLISHCHAPTER - INTEGRALSEXERCISE - All Questions764videos
INTEGRALS
- BOOK - CENGAGE ENGLISHCHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Archives (Numerical Value type)2videos
INVERSE TRIGONOMETRIC FUNCTIONS
Similar Questions
If the position vectors of the points A,B and C be a,b and 3a-2b respectively, then prove that the points A,B and C are collinear.
View Solution→a,→b,→c are the position vectors of vertices A, B, C respectively of a paralleloram, ABCD, ifnd the position vector of D.
View SolutionIf a,b and c are the position vectors of the vertices A,B and C of the ΔABC, then the centroid of ΔABC is
View SolutionLet A,B,C be vertices of a triangle ABC in which B is taken as origin of reference and position vectors of A and C are →aand→c respectively. A line AR parallel to BC is drawn from A PR (P is the mid point of AB) meets AC and Q and area of triangle ACR is 2 times area of triangle ABC Positon vector of Q for position vector of R in (1) is (A) 2→a+3→c5 (B) 3→a+2→c5 (C) →a+2→c5 (D) none of these
View SolutionLet A, B, C respresent the vertices of a triangle, where A is the origin and B and C have position b and c respectively. Points M, N and P are taken on sides AB, BC and CA respectively, such that (AM)/(AB)=(BN)/(BC)=(CP)/(CA)=alpha Q. AN+BP+CM is
View SolutionLet A,B,C be vertices of a triangle ABC in which B is taken as origin of reference and position vectors of A and C are →aand→c respectively. A line AR parallel to BC is drawn from A PR (P is the mid point of AB) meets AC and Q and area of triangle ACR is 2 times area of triangle ABC Position vector of R in terms →aand→c is (A) →a+2→c (B) →a+3→c (C) →a+→c (D) →a+4→c
View SolutionIf →a, →b, →c are position vectors of the vertices A, B and C respectively, of a triangle ABC, write the value of →AB+→BC+→CA.
View SolutionA (-1, 0), B (1, 3) and D (3, 5) are the vertices of a parallelogram ABCD. Find the co-ordinates of vertex C.
View SolutionIn the pelvic girdle of man A,B,C,D and E respectively represent
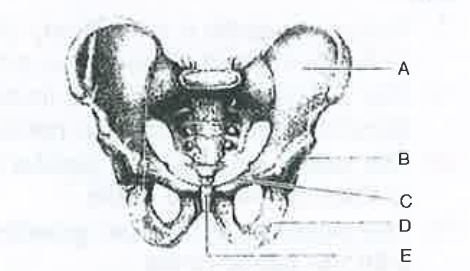 View Solution
View SolutionIf →a,→b,→c are the position vectors of the vertices. A,B,C of a triangle ABC. Then the area of triangle ABC is
View Solution

