Let ABC be a triangle whose centroid is G, orthocentre is H and circumcentre is the origin 'O'. If D is any point in the plane of the triangle such that no three of O,A,C and D are collinear satisfying the relation.
AD+BD+CH+3HB=λHD, then what is the value of the scalar Δ.
The correct Answer is:2
L.H.S = →d−→a+→d−→b+→h−→c+3(→g−→h)
=2→d−(→a+→b+→c)+3(→a+→b+→c)3−2→h
=2→d−2→h=2(→d−→h)=2−−→HD
⇒λ=2
Topper's Solved these Questions
- BOOK - CENGAGE ENGLISHCHAPTER - INTRODUCTION TO VECTORS EXERCISE - ARCHIVES SUBJECTIVE TYPE9videos
INTRODUCTION TO VECTORS
- BOOK - CENGAGE ENGLISHCHAPTER - INTRODUCTION TO VECTORS EXERCISE - FILL IN THE BLANKS2videos
INTRODUCTION TO VECTORS
- BOOK - CENGAGE ENGLISHCHAPTER - INTRODUCTION TO VECTORS EXERCISE - LINKED COMPREHENSION TYPE11videos
INTRODUCTION TO VECTORS
- BOOK - CENGAGE ENGLISHCHAPTER - INTEGRALSEXERCISE - All Questions764videos
INTEGRALS
- BOOK - CENGAGE ENGLISHCHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Archives (Numerical Value type)2videos
INVERSE TRIGONOMETRIC FUNCTIONS
Similar Questions
Let ABC be a triangle whose centroid is G, orthocentre is H and circumcentre is the origin 'O'. If D is any point in the plane of the triangle such that no three of O,A,C and D are collinear satisfying the relation. AD+BD+CH+3HG=λHD, then what is the value of the scalar λ.
View SolutionLet ABC be a triangle having its centroid its centroid at G. If S is any point in the plane of the triangle, then −→SA+−−→SB+−−→SC=
View SolutionLet ABC be a triangle having its centroid its centroid at G. If S is any point in the plane of the triangle, then −→SA+−−→SB+−−→SC=
View SolutionIf D any point on the BC of an isosceles triangle ABC then prove that AB>AD and AC>AD.
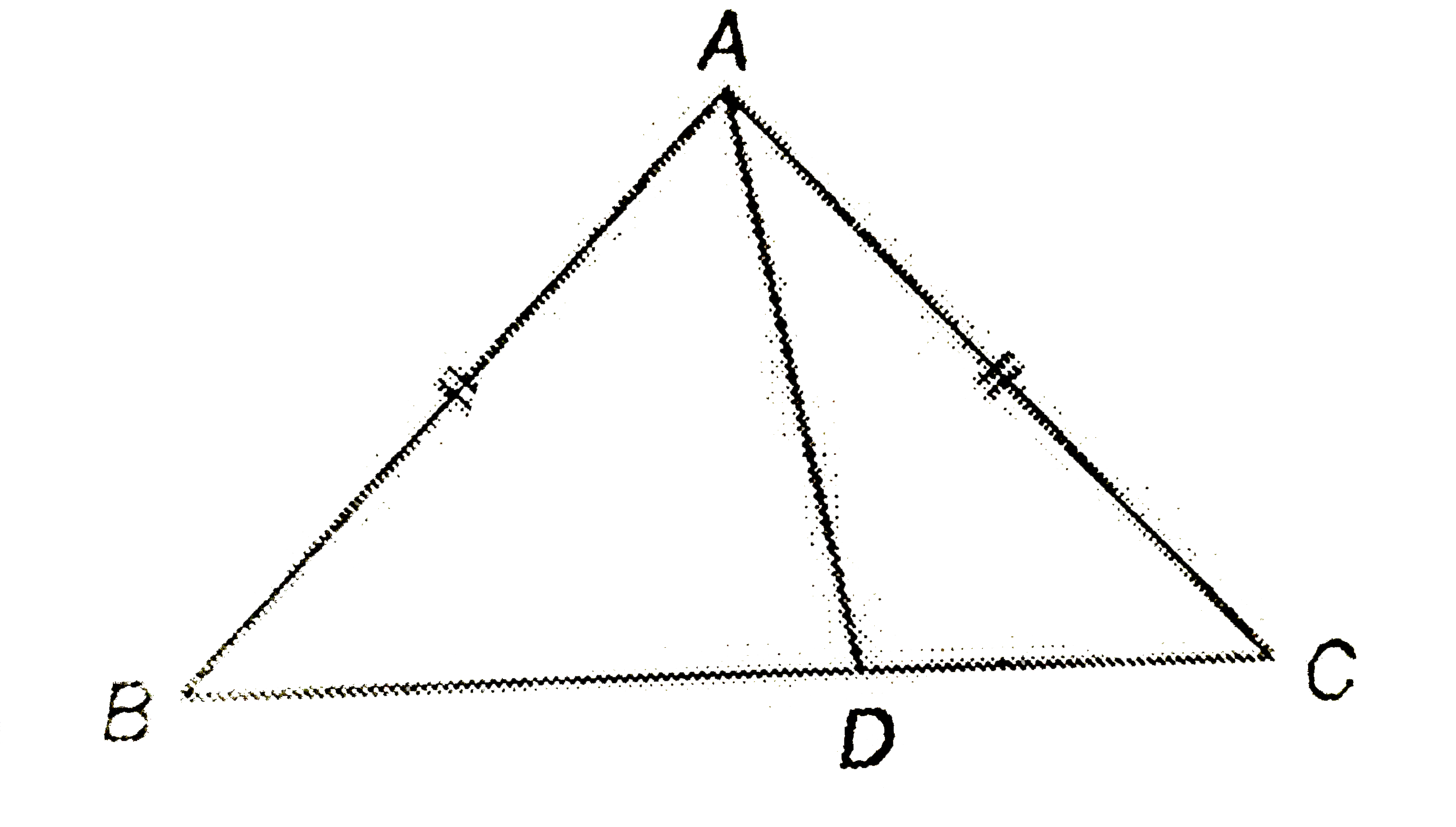View SolutionABC is a triangle whose circumcentre, incentre and orthocentre are O, I and H respectively which lie inside the triangle, then :
View SolutionletABC be a right angled triangle at C.If the inscribed circle touches the side ABat D and (AD)(BD)=11, then find the area of triangle ABC..
View SolutionletABC be a right angled triangle at C.If the inscribed circle touches the side ABat D and (AD)(BD)=11, then find the area of triangle ABC..
View SolutionLet ABC be an acute angled triangle whose orthocentre is at H. If altitude from A is produced to meet the circumcircle of triangle ABC at D , then prove HD=4RcosBcosC
View SolutionLet ABC be a triangle with ∠B=900 . Let AD be the bisector of ∠A with D on BC. Suppose AC=6cm and the area of the triangle ADC is 10cm2. Find the length of BD.
View SolutionLet ABC be a triangle with ∠B=900 . Let AD be the bisector of ∠A with D on BC. Suppose AC=6cm and the area of the triangle ADC is 10cm2. Find the length of BD.
View Solution