If D any point on the BC of an isosceles triangle ABC then prove that AB>AD and AC>AD.
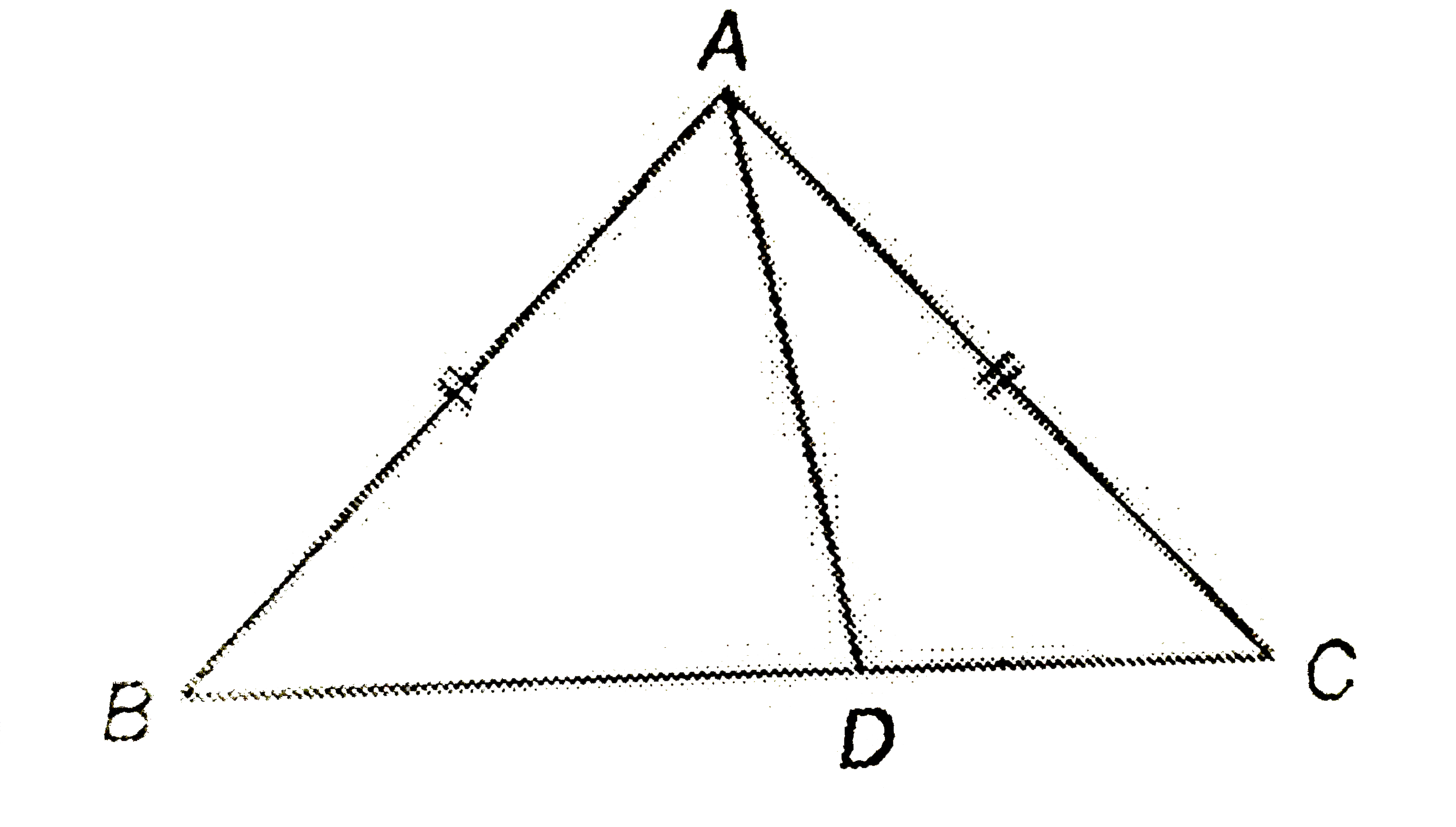
In ΔABC
AB=AC
⇒ ∠ACB=∠ABC ...(1)
In ΔABD
∠ADC=∠ABD+∠BAD (∠ADC is exterior angle)
⇒ ∠ADC>∠ABD
⇒ ∠ADC>∠ACD [from (1)]
⇒ Ac>AD Hence Proved.
Again in ΔACD
∠ADB=∠ACD+∠CAD (∠ADB is exterior angle)
⇒ ∠ADB>∠ACD
⇒ ∠ADB>∠ABD [from (1)]
⇒ AB>AD Hence Proved.
Topper's Solved these Questions
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - TRIANGLESEXERCISE - Problems From NCERT/exemplar5videos
TRIANGLES
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - TRIANGLESEXERCISE - Exercise 7a35videos
TRIANGLES
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - SURFACE AREA AND VOLUMEEXERCISE - Revision Exercise (long Answer Questions)10videos
SURFACE AREA AND VOLUME
Similar Questions
AD is a median of triangle ABC. Prove that : AB+AC>2AD
View SolutionD is a point in side BC of triangle ABC. If AD>AC, show that AB>AC.
View SolutionAD is a median of triangle ABC. Prove that : AB+BC+AC>2AD
View SolutionIn following figure if AD if the bisector of ∠ABC, then prove that AB>BD
 View Solution
View SolutionIf D is a Point on the side BC of a ΔABC such that AD bisects ∠BAC. Then
View SolutionD, E and F are the mid-points of the sides AB, BC and CA of an isosceles triangle ABC in which AB = BC. Prove that ΔDEF is also isosceles.
View SolutionP is any point inside the triangle ABC. Prove that : ∠BPC>∠BAC.
View SolutionIn figure ,D and E are Points on side BC of a ΔABC such that BD=CE and AD=AE. Show that ΔABD≅ΔACE.
 View Solution
View SolutionIn the figure, AD is perpendicular to BC, prove that AB+AC>2AD.
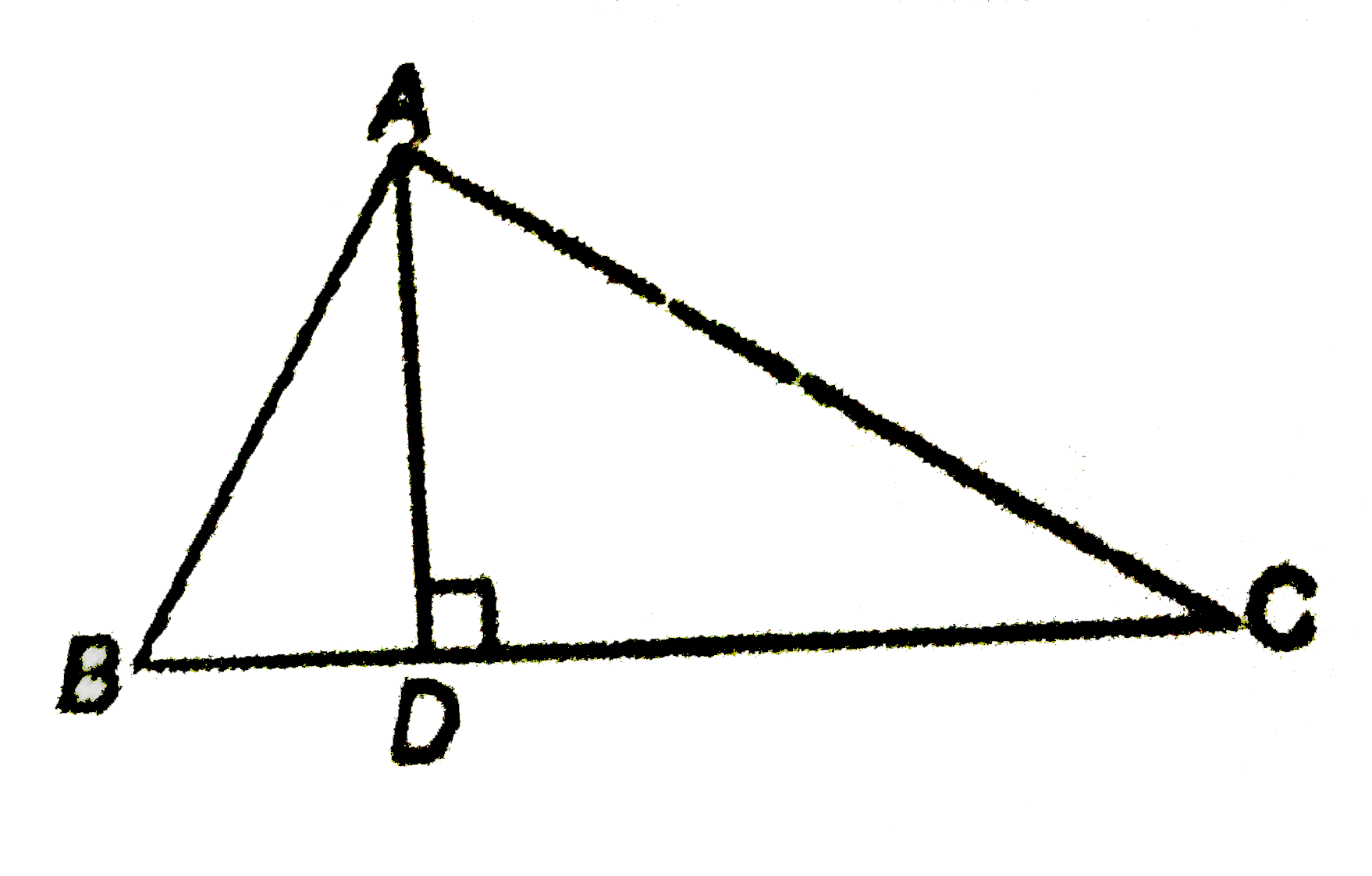 View Solution
View SolutionABC is an isosceles triangle with AB = AC = 2a and BC = a . If AD⊥BC, find the length of AD .
View Solution

