If f(x)=ax2+bx+c , where a≠0,b,c∈ R , then which of
the following conditions implies that f(x) has real roots?
a+ b + c = 0
a and c are of opposite signs
4ac−b2<0
a and b are of opposite signs
The correct Answer is:1,2,3,
To determine the conditions under which the quadratic function f(x)=ax2+bx+c has real roots, we need to analyze the discriminant of the quadratic equation. The discriminant D is given by:
D=b2−4ac
For the quadratic equation to have real roots, the discriminant must be greater than or equal to zero:
D≥0
This means:
b2−4ac≥0
Now, let's analyze the given conditions one by one to see which of them imply that f(x) has real roots.
Step 1: Analyze the first condition a+b+c=0
If a+b+c=0, then substituting x=1 into the function gives:
f(1)=a(1)2+b(1)+c=a+b+c=0
This means that x=1 is a root of the equation. Since one root exists, the quadratic must have real roots. Thus, this condition implies that f(x) has real roots.
Step 2: Analyze the second condition ac<0
If ac<0, it means that a and c have opposite signs. This implies that the parabola opens upwards (if a>0) and crosses the x-axis (if c<0), or it opens downwards (if a<0) and also crosses the x-axis (if c>0).
Using the discriminant:
D=b2−4ac
Since ac<0, −4ac>0. Therefore, b2−4ac>0 implies that the discriminant is positive, indicating that there are two distinct real roots. Thus, this condition also implies that f(x) has real roots.
Step 3: Analyze the third condition 4ac−b2<0
Rearranging this condition gives:
b2−4ac>0
This is the same condition we derived from the discriminant. Therefore, this condition also implies that f(x) has real roots.
Step 4: Analyze the fourth condition ab<0
If ab<0, it means that a and b have opposite signs. However, this condition alone does not provide information about the value of c. Therefore, we cannot conclude that the quadratic has real roots based solely on this condition. Thus, this condition does not imply that f(x) has real roots.
Conclusion
The conditions that imply that f(x) has real roots are:
1. a+b+c=0
2. ac<0
3. 4ac−b2<0
The fourth condition ab<0 does not imply that f(x) has real roots.
2. ac<0
3. 4ac−b2<0
Topper's Solved these Questions
- BOOK - CENGAGE ENGLISHCHAPTER - THEORY OF EQUATIONSEXERCISE - Linked Comprechension Type37videos
THEORY OF EQUATIONS
- BOOK - CENGAGE ENGLISHCHAPTER - THEORY OF EQUATIONSEXERCISE - MATRIX MATCH TYPE6videos
THEORY OF EQUATIONS
- BOOK - CENGAGE ENGLISHCHAPTER - THEORY OF EQUATIONSEXERCISE - Single Correct Answer Type : Exercise89videos
THEORY OF EQUATIONS
- BOOK - CENGAGE ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - ARCHIVES (NUMERICAL VALUE TYPE)1videos
STRAIGHT LINES
- BOOK - CENGAGE ENGLISHCHAPTER - THREE DIMENSIONAL GEOMETRYEXERCISE - All Questions294videos
THREE DIMENSIONAL GEOMETRY
Similar Questions
Let f(x)=x3+ax2+bx+c and g(x)=x3+bx2+cx+a, where a, b, c are integers. Suppose that the following conditions hold-
(a) f(1)=0,
(b) the roots of g(x) = 0 are the squares of the roots of f(x) = 0. Find the value of: a2013+b2013+c2013View SolutionIf f(x)=a+bx+cx2 where a,b,c∈R then ∫1of(x)dx
View Solution
Knowledge Check
- Question 1 - Select One
If f(x)=ax2+bx+c,a≠0 and a, b , and c are all negative , which could be the graph of f(x) ?
A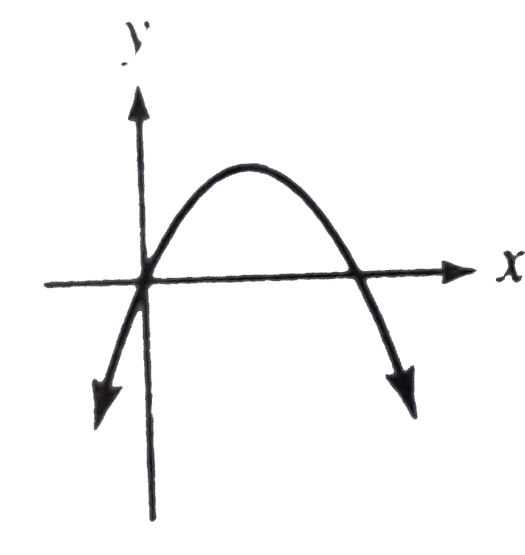 B
B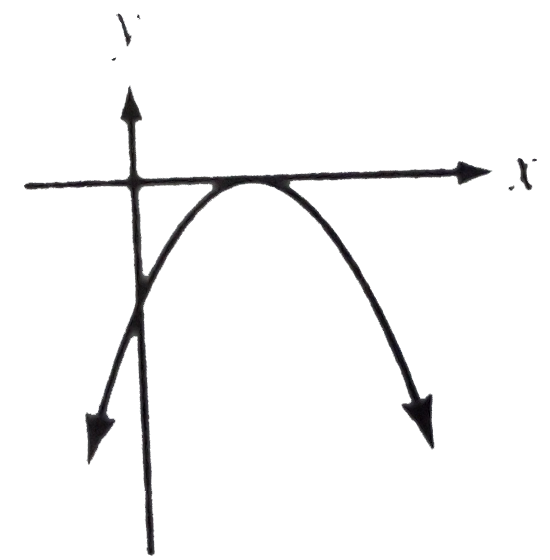 C
C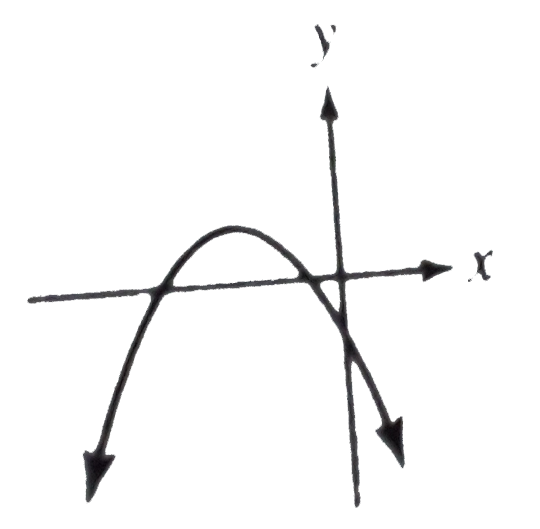 D
D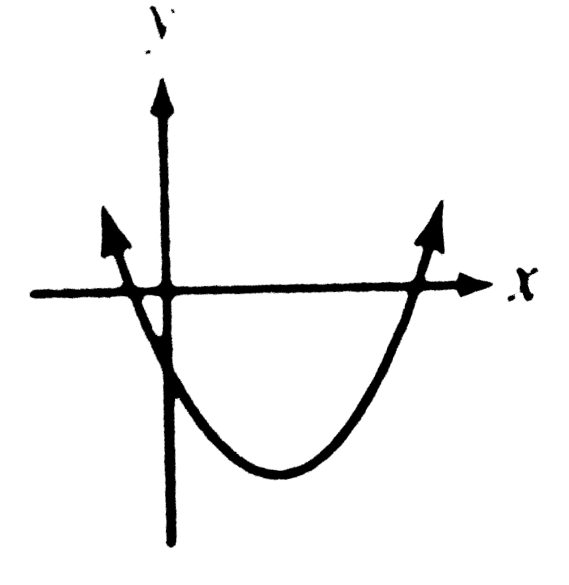
Let f(x)=ax2−bx+c2,b≠0andf(x)≠0 for all x∈R. Then
View SolutionLet f(x) =ax3+bx2+cx+d,a≠0, where a, b, c, d∈R. If f(x) is one-one and onto, then which of the following is correct ?
View SolutionIf ax2+bx+c=0 has no real roots and a, b, c ∈ R such that a+c>0, then
View SolutionLet f(x)=ax2+bx+c, where a,b,c∈R,a≠0. Suppose |f(x)|≤1,x∈[0,1], then
View SolutionLet f:[0,5]→[0,5) be an invertible function defined by f(x)=ax2+bx+C, where a,b,c∈R,abc≠0, then one of the root of the equation cx2+bx+a=0 is:
View SolutionLet f:[0,5]→[0,5) be an invertible function defined by f(x)=ax2+bx+C, where a,b,c∈R,abc≠0, then one of the root of the equation cx2+bx+a=0 is:
View SolutionLet f(x)=ax2+bx+c, g(x)=ax2+px+q, where a, b, c, q, p∈R and b≠p. If their discriminants are equal and f(x)=g(x) has a root α, then
View Solution

