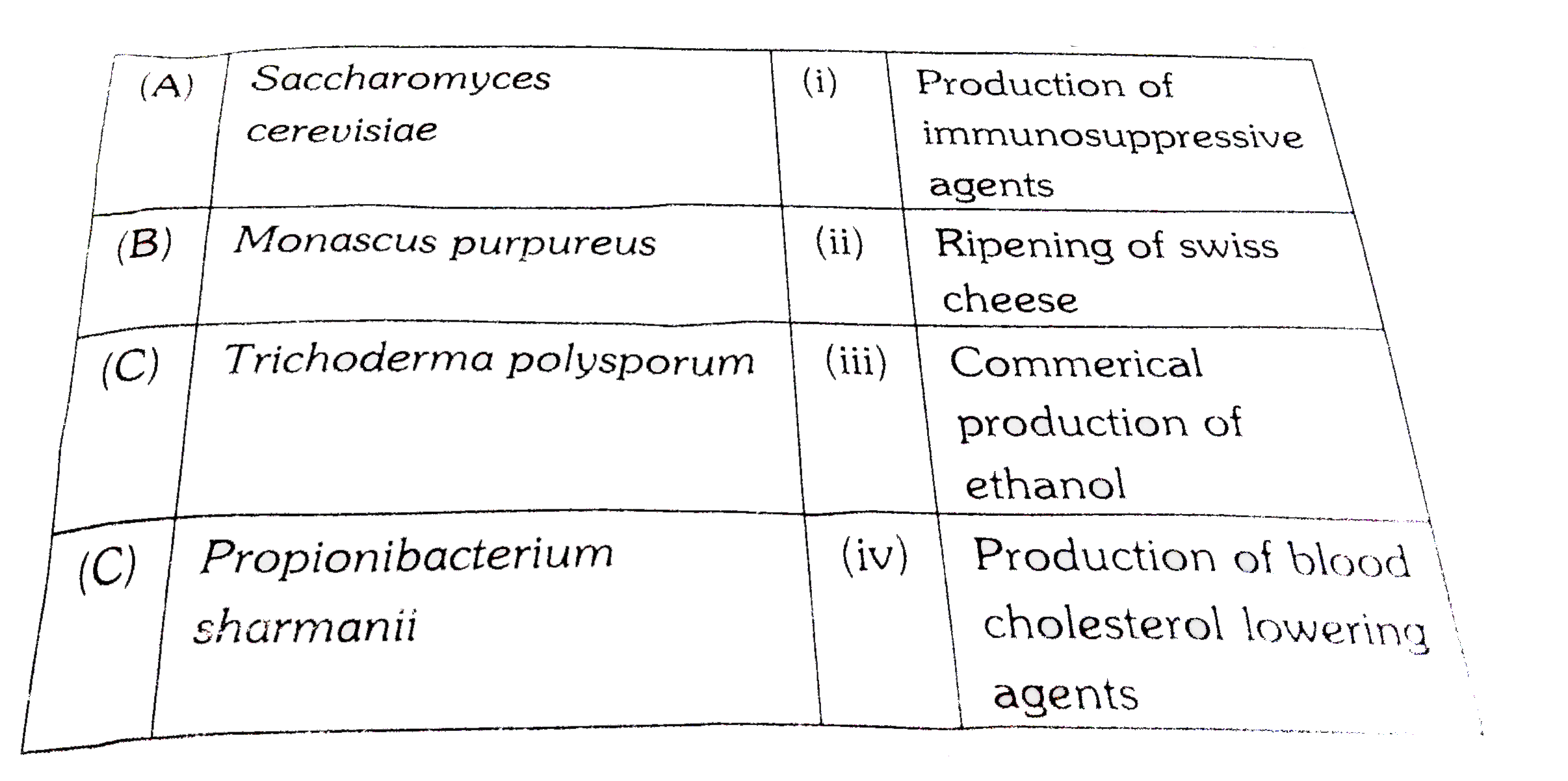Match the following lists:

The correct Answer is:a→s;b→p;c→q;d→r
a→s,b→p,c→q,d→r
(a) x2ax+b=0 has root lapha. Hence.
α2+aα+b=0 (1)
x2+px+q=0 has root −α. Hence,
α2−pα+q= (2)
Eliminating α from (1) and (2), we get
(q−b)2=(aq+bp)(−p−a)
or (q−b)2=−(aq+pb)(p+a)
(b) x2ax+b=0 has root α. Hence,
α2+aα+b=0 (1)
x2+px+q=0 has root 1/α. Hence,
qα2+pα+1=0 (2)
Eliminating α from (1) and (2), we get
(1−bq)2=(a−pb)(p−aq)
(c) x2+ax+b=0 has roots, α,β. Hence,
α2+aα+b=0 (1)
x2+px+q=0 has roots −2/α,γ. Hence,
qα2−2pα+4=0 (2)
Eliminating α from (1) and (2), we et
(4−bq)2=(4a+2pb)(−2p−aq)
(d) x2+ax+b=0 has roots α,β. Hence,
α2+aα+b=0 (1)
x2+px+q=0 has roots −1/2α,γ. Hence,
4qα2−2pα+1=0 (2)
Elimintaing α from (1) and (2), we get
(1−4bq)2=(a+2bp)(−2p−4aq)
Topper's Solved these Questions
- THEORY OF EQUATIONSBOOK - CENGAGE ENGLISHCHAPTER - THEORY OF EQUATIONSEXERCISE - NUMERICAL VALUE TYPE
43 Videos
- THEORY OF EQUATIONSBOOK - CENGAGE ENGLISHCHAPTER - THEORY OF EQUATIONSEXERCISE - Archives JEE MAIN (single correct Answer Type )
7 Videos
- THEORY OF EQUATIONSBOOK - CENGAGE ENGLISHCHAPTER - THEORY OF EQUATIONSEXERCISE - Linked Comprechension Type
37 Videos
- STRAIGHT LINESBOOK - CENGAGE ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - ARCHIVES (NUMERICAL VALUE TYPE)
1 Videos
- THREE DIMENSIONAL GEOMETRYBOOK - CENGAGE ENGLISHCHAPTER - THREE DIMENSIONAL GEOMETRYEXERCISE - All Questions
294 Videos
Similar Questions
Knowledge Check
Match the following list of bacteria and their commercially important products.
BacteriumProduct(i)Aspergillus niger(A)Lactic acid(ii)Acetobacter aceti(B)Butyric acid(iii)Clostridium butylicum(C)Acetic acid(iv)Lactobacillus(D)Citric acid
Choose the correct match.Ai−(B),ii−(C),iii−(D),iv−(A)Bi−(B),ii−(D),iii−(C),iv−(A)Ci−(D),ii−(C),iii−(B),iv−(A)Di−(D),ii−(A),iii−(C),−iv−(B)
Match the following list of bioactive sub- stances and their roles
Choose the correct match

View SolutionMatch the following list of bacteria and their commercially important products
Choose the correct match

View SolutionMatch the following list of animals with their level of organisation :
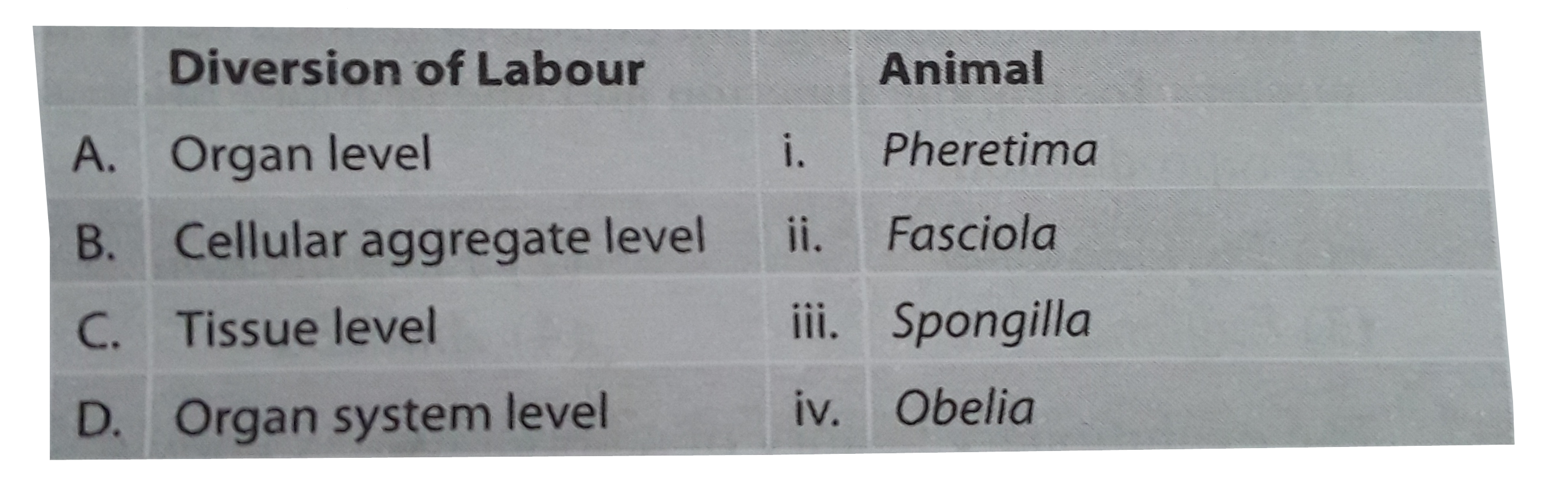
Choose the correct match showing division of labour with animals.
View SolutionMatch the following list of animals with their level of organisation.
Choose the correct match sryowing division of labour with animal example.

View SolutionMatch the following list of animals with their level of organisation.
Division of LabourAnimalA.Organ leveli.PheretimaB.Cellular aggregate levelii.FasciolaC.Tissue leveliii.SpongillaD.Organ system leveliv.Obelia
Choose the correct match showing division of labour with animal example.
View SolutionMatch the following list of bioactive substances and their roles.
Bioactive substanceRole(i)Statin(A)Removal of oil stains(ii)CyclosporinA(B)Removal of clots from blood vessels(iii)Streptokinase(C)Lowering of blood cholesterol(iv)Lipase(D)Immuno-suppressive agent
Choose the correct match.
View SolutionMatch the following list of bacteria and their commercially important products.
BacteriumProduct(i)Aspergillus niger(A)Lactic acid(ii)Acetobacter aceti(B)Butyric acid(iii)Clostridium butylicum(C)Acetic acid(iv)Lactobacillus(D)Citric acid
Choose the correct match.
View Solution