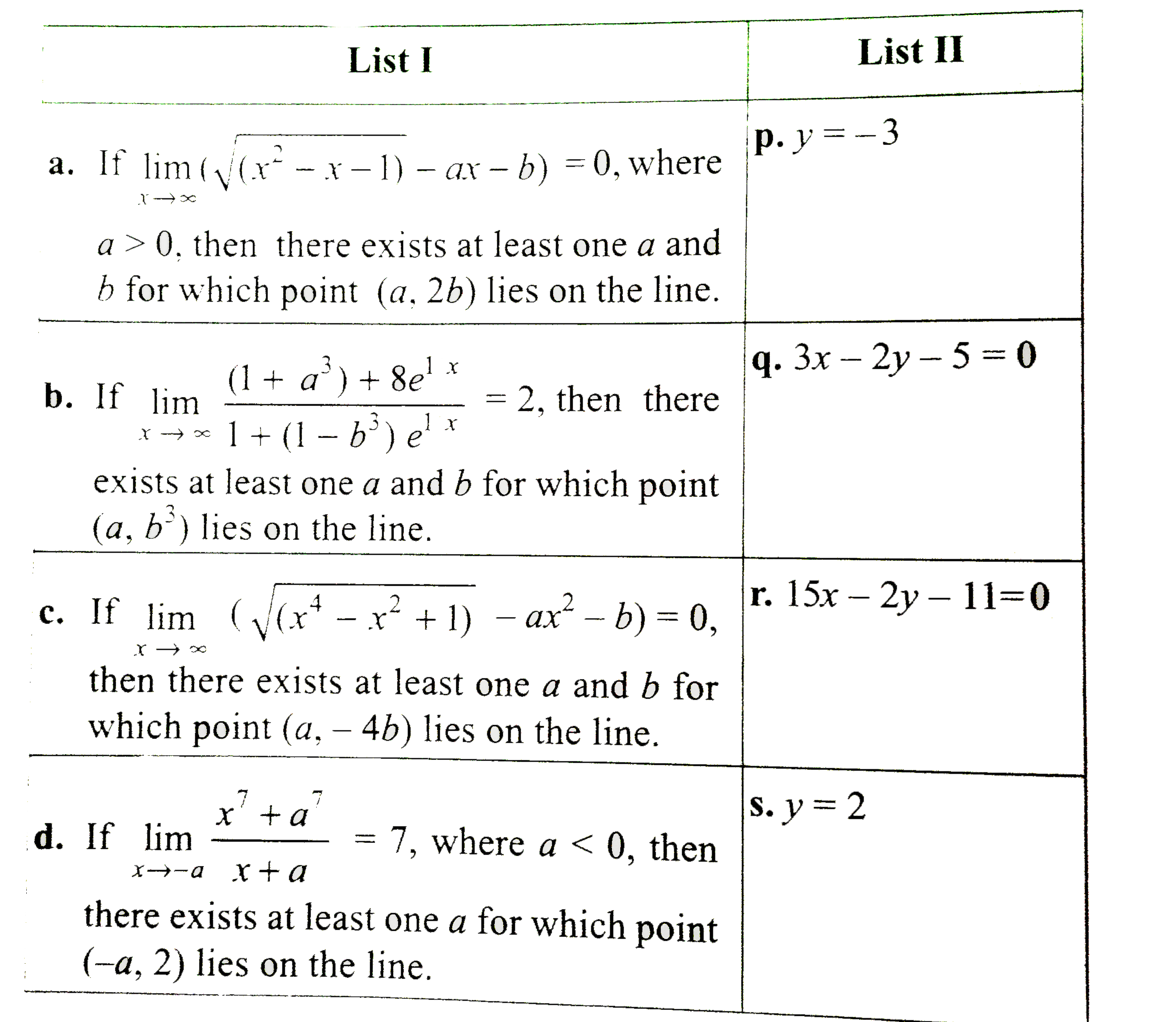
Match the following for lists:

Text Solution
The correct Answer is:a→r;b→r;c→q;d→p
a→r,b→r,c→q,d→p
(m−2)x2−(8−2m)x−(8−3m)=0 has roots of opposite signs. The product of roots is
−8−3mm−2<0
or 3m−8m−2<0
or 2<m<8/3
(b) Exactly one root of equation x2−m(2x−8)−15=0 lies in interval (0,1).
f(0)f(1)<0
⇒(0−m(−8)−14)(1−m(−6)−15)<0
⇒(8m−15)(6m−14)<0
⇒15/8<m<7/3
(c) x2+2(m+1)x+9m−5=0 has both roots negative. Hence, sum of roots is
−2(m+1)<orm>−1 (1)
Product of roots is
9m−5>0⇒m>5/9 (2)
Discriminant,
D≥0⇒4(m+1)2−4(9m−5)≥0
⇒m2−7m+6≥0
⇒m≤1orm≥0 (3)
Hence, for (1), (2),and (3), we get
m∈(59,1]∪[6,∞)
(d) f(x)=x2+2(m−1)x+m+5=0 has one root less than 1 and the other root greater than 1. Hence,
f(1)<0
⇒1+2(m−1)+m+5<0
⇒m<−4/3
|
Topper's Solved these Questions
- THEORY OF EQUATIONSBOOK - CENGAGE ENGLISHCHAPTER - THEORY OF EQUATIONSEXERCISE - NUMERICAL VALUE TYPE
43 Videos
- THEORY OF EQUATIONSBOOK - CENGAGE ENGLISHCHAPTER - THEORY OF EQUATIONSEXERCISE - Archives JEE MAIN (single correct Answer Type )
7 Videos
- THEORY OF EQUATIONSBOOK - CENGAGE ENGLISHCHAPTER - THEORY OF EQUATIONSEXERCISE - Linked Comprechension Type
37 Videos
- STRAIGHT LINESBOOK - CENGAGE ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - ARCHIVES (NUMERICAL VALUE TYPE)
1 Videos
- THREE DIMENSIONAL GEOMETRYBOOK - CENGAGE ENGLISHCHAPTER - THREE DIMENSIONAL GEOMETRYEXERCISE - All Questions
294 Videos
Similar Questions
Knowledge Check
Match the following lists.
 AABC123BABC213CABC132DABC312
AABC123BABC213CABC132DABC312Match the following lists .
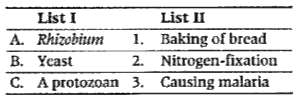 AABC123BABC213CABC132DABC312
AABC123BABC213CABC132DABC312