A right circular cone with radius R and height H contains a liquid which evaporates at a rate proportional to its surface area in contact with air (proportionality constant k is positive). Suppose that r(t) is the radius of the liquid cone at time t. The time after which the cone is empty is
To solve the problem of determining the time after which the cone is empty, we will follow these steps:
Step 1: Set up the relationship between volume and surface area
The volume V of a right circular cone is given by the formula:
V=13πr2h
where r is the radius of the liquid cone at time t and h is the height of the liquid cone at that time.
Step 2: Express height in terms of radius
Using the similarity of triangles, we can express the height h of the liquid cone in terms of the radius r:
rR=hH⟹h=HRr
Step 3: Find the surface area in contact with air
The surface area A of the liquid in contact with air is:
A=πr2
Step 4: Set up the differential equation
According to the problem, the rate of change of volume with respect to time is proportional to the surface area:
−dVdt=k⋅A=kπr2
Substituting the volume V gives:
−ddt(13πr2h)=kπr2
Step 5: Substitute h in the volume equation
Substituting h=HRr into the volume equation:
V=13πr2(HRr)=H3Rπr3
Thus, we have:
−ddt(H3Rπr3)=kπr2
Step 6: Differentiate the volume with respect to time
Differentiating gives:
−HRπr2drdt=kπr2
Cancelling πr2 (assuming r≠0):
−HRdrdt=k
Step 7: Rearranging the equation
Rearranging gives:
drdt=−kRH
Step 8: Integrate to find r(t)
Integrating both sides:
∫dr=−kRH∫dt
This results in:
r=−kRHt+C
Step 9: Determine the constant C
At t=0, let r=R:
R=C⟹C=R
Thus, the equation becomes:
r=−kRHt+R
Step 10: Find the time T when the cone is empty
The cone is empty when r=0:
0=−kRHT+R
Solving for T:
kRHT=R⟹T=Hk
Final Answer
The time after which the cone is empty is:
T=Hk
The volume V of a right circular cone is given by the formula:
V=13πr2h
where r is the radius of the liquid cone at time t and h is the height of the liquid cone at that time.
Using the similarity of triangles, we can express the height h of the liquid cone in terms of the radius r:
rR=hH⟹h=HRr
The surface area A of the liquid in contact with air is:
A=πr2
According to the problem, the rate of change of volume with respect to time is proportional to the surface area:
−dVdt=k⋅A=kπr2
Substituting the volume V gives:
−ddt(13πr2h)=kπr2
Substituting h=HRr into the volume equation:
V=13πr2(HRr)=H3Rπr3
Thus, we have:
−ddt(H3Rπr3)=kπr2
Differentiating gives:
−HRπr2drdt=kπr2
Cancelling πr2 (assuming r≠0):
−HRdrdt=k
Rearranging gives:
drdt=−kRH
Integrating both sides:
∫dr=−kRH∫dt
This results in:
r=−kRHt+C
At t=0, let r=R:
R=C⟹C=R
Thus, the equation becomes:
r=−kRHt+R
The cone is empty when r=0:
0=−kRHT+R
Solving for T:
kRHT=R⟹T=Hk
The time after which the cone is empty is:
T=Hk
Topper's Solved these Questions
- DIFFERENTIAL EQUATIONSBOOK - CENGAGE ENGLISHCHAPTER - DIFFERENTIAL EQUATIONSEXERCISE - SINGLE CORRECT ANSWER TYPES
74 Videos
- DIFFERENTIAL EQUATIONSBOOK - CENGAGE ENGLISHCHAPTER - DIFFERENTIAL EQUATIONSEXERCISE - MULTIPLE CORRECT ANSWERS TYPE
17 Videos
- DIFFERENTIAL EQUATIONSBOOK - CENGAGE ENGLISHCHAPTER - DIFFERENTIAL EQUATIONSEXERCISE - CONCEPT APPLICATION EXERCISES 10.8
7 Videos
- DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS BOOK - CENGAGE ENGLISHCHAPTER - DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS EXERCISE - Multiple correct answers type
11 Videos
- DIFFERENTIATIONBOOK - CENGAGE ENGLISHCHAPTER - DIFFERENTIATIONEXERCISE - Archives
14 Videos
Similar Questions
Spherical rain drop evaporates at a rate proportional to its surface area. The differential equation corresponding to the rate of change of the radius of the rain drop if the constant of proportionality is K>0 is
View SolutionThe cone of radius R and height H is hanging inside a liquid of density by means of a string a shwon in the figure.

View Solution
Knowledge Check
If a right circular cone has a lateral surface area of 6π and a slant height of 6, what is the radius of the base ?
A0.50B0.75C1.00D1.25
An inverted cone of height H, and radius R is pointed at bottom. It is completely filled with a volatile liquid. If the rate of evaporation is directly proportional to the surface area of the liquid in contact with air (constant of proportionality k > 0). Find the time in which whole liquid evaporates.
View SolutionFind the total surface area of a right circular cone with radius 6cm and height 8cm.
View Solution
A right circular cone, with radius and height 8 and 6 respectively , is cut parallel at the middle of the height to get a smaller cone and a frustum. By what percentage, to the nearest integer, is the combined total surface area of the smaller cone less than of the frustum?
View SolutionA cone of radius R and height H, is hanging inside a liquid of density ρ by means of a string as shown in figure. The force due to the liquid acting on the slant surface of the cone is
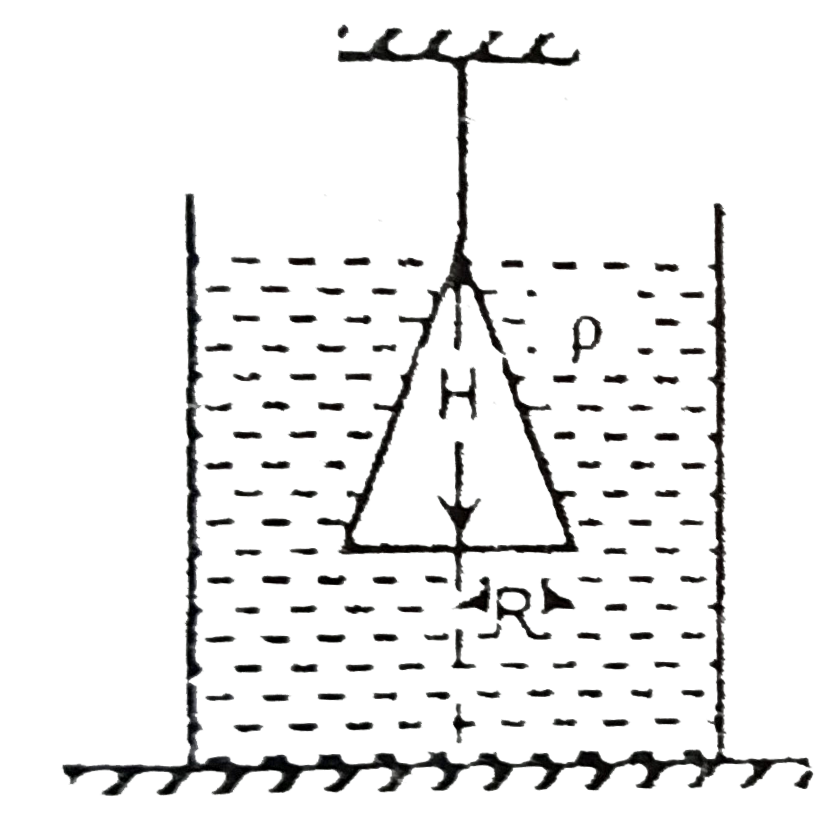
View SolutionThe total surface area of a cone whose radius is r2 and slant height 2l is
View SolutionThe surface area of a spherical balloon being inflated, changes at a rate proportional to time t. If initially its radius is 1 unit and after 3 secons it is 2 units, find the radius after t seconds.
View SolutionThe radius of base of a cone is r and height is h. Find its volume.
View Solution
