An inverted cone of height H, and radius R is pointed at bottom. It is completely filled with a volatile liquid. If the rate of evaporation is directly proportional to the surface area of the liquid in contact with air (constant of proportionality k > 0). Find the time in which whole liquid evaporates.
Step by step video & image solution for An inverted cone of height H, and radius R is pointed at bottom. It is completely filled with a volatile liquid. If the rate of evaporation is directly proportional to the surface area of the liquid in contact with air (constant of proportionality k gt 0). Find the time in which whole liquid evaporates. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
A right circular cone with radius R and height H contains a liquid which evaporates at a rate proportional to its surface area in contact with air (proportionality constant k is positive). Suppose that r(t) is the radius of the liquid cone at time t. The time after which the cone is empty is
View SolutionSpherical rain drop evaporates at a rate proportional to its surface area. The differential equation corresponding to the rate of change of the radius of the rain drop if the constant of proportionality is K>0 is
View SolutionA solid cone of height H and base radius H2 floats in a liquid of density ρ. It is hanging from the ceiling with the help of a string. The force by the fluid on the curved surface of the cone is (P0= atmospheric pressure)
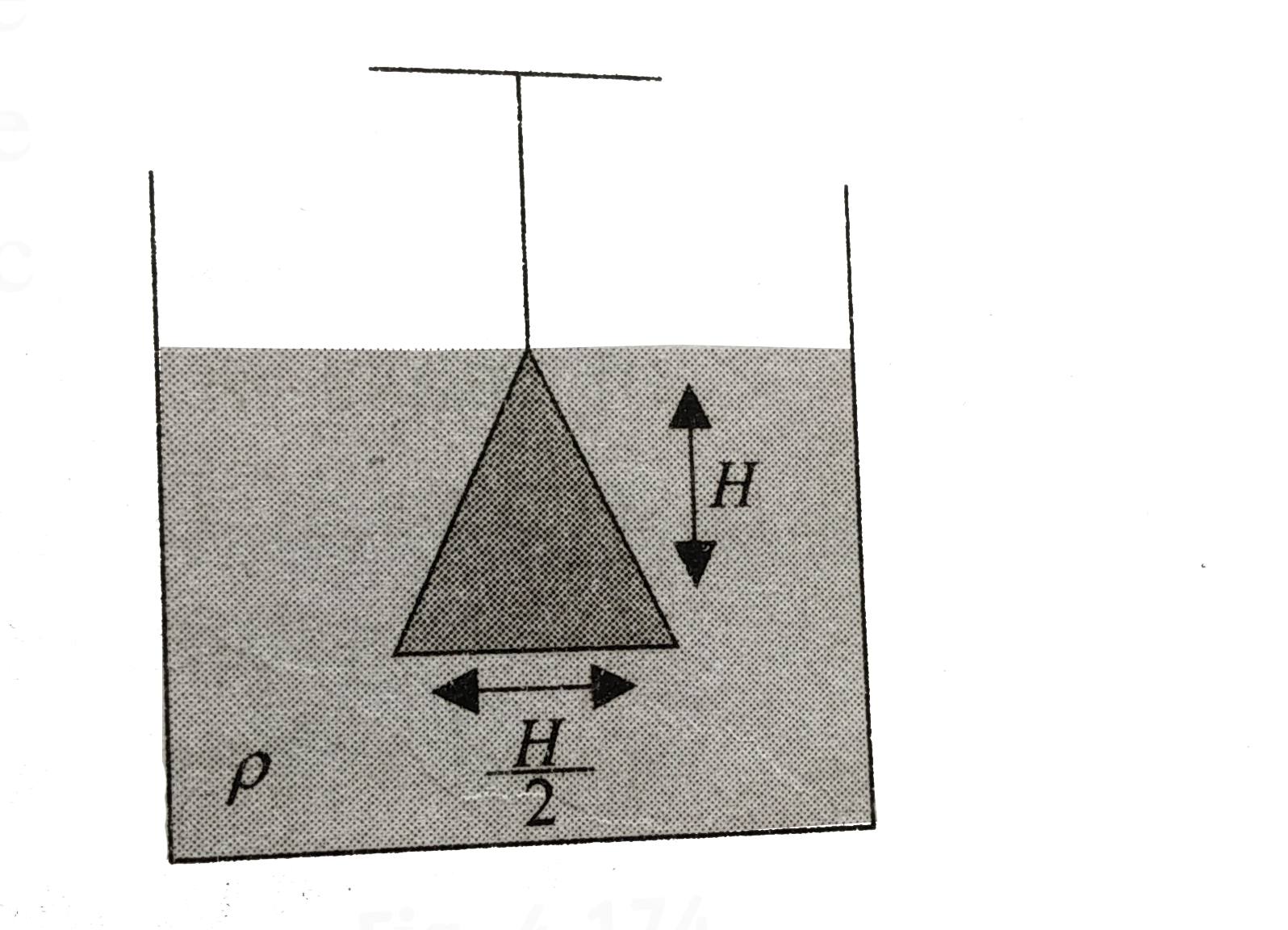
View SolutionA cylindrical container of radius 'R' and height 'h' is completely filled with a liquid. Two horizontal L-shaped pipes of small cross-sectional area 'a' are connected to the cylinder as shown in the figure. Now the two pipes are opened and fluid starts coming out of the pipes horizontally in opposite directions. Then the torque due to ejected liquid on the system is

View SolutionA cone of radius R and height H, is hanging inside a liquid of density ρ by means of a string as shown in figure. The force due to the liquid acting on the slant surface of the cone is
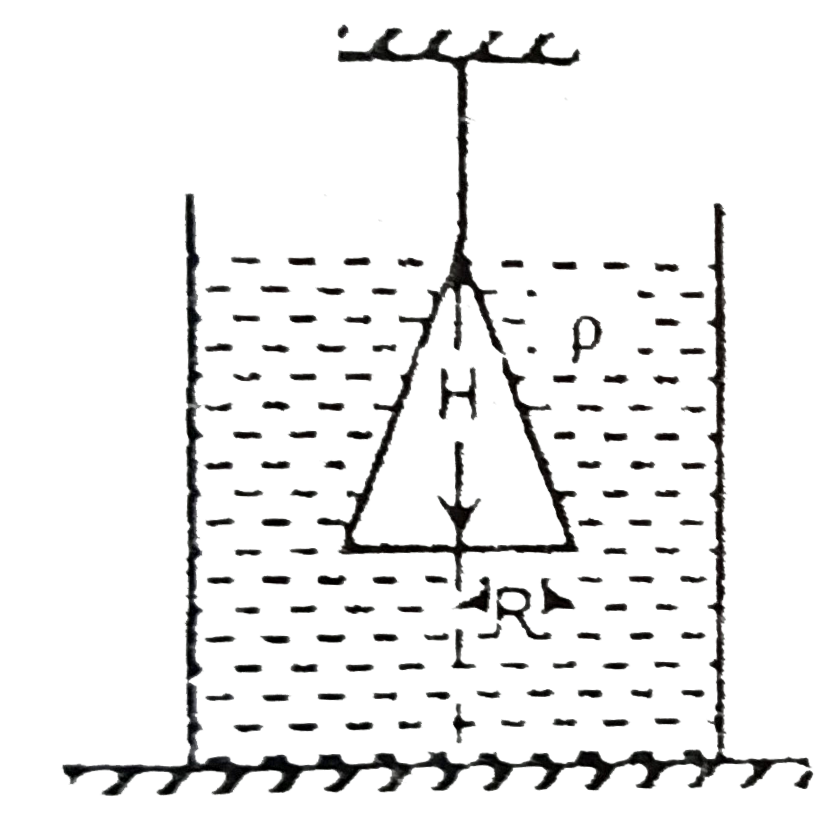
View SolutionA horizontal thin tube of length 2L completely filled with a liquid of density δ rotates about a vertical axis passing through one of its end and along the diameter of its side face with an constant angular velocity ω. Two vertical thin long tubes are fitted with the horizontal tube to measure the pressure difference between points A and B which are at same horizontal level as shown. Neglect viscous forces and surfaces tension of liquid.

The difference in the heights (h) of the liquid column in the two vertical thin tubes is :
View SolutionIn the adjacent figure a cylindrical vessel of mass M and cross - sectional area A is placed inverted on a fixed smooth piston of same cross - sectional area fixed to the ground . The space between the cylinder and priston is completely filled with liquid of density ρ . There is a small office of cross - sectional area a (a<<A) at the top top portion of this vessel . ( intially length of the liquid column in the vessel is H )
Speed of the liquid with which it comes out of the vessel is

View SolutionIn the adjacent figure a cylindrical vessel of mass M and cross - sectional area A is placed inverted on a fixed smooth piston of same cross - sectional area fixed to the ground . The space between the cylinder and priston is completely filled with liquid of density ρ . There is a small office of cross - sectional area a (a<<A) at the top top portion of this vessel . ( intially length of the liquid column in the vessel is H ).Find the speed of the vessel with which it move
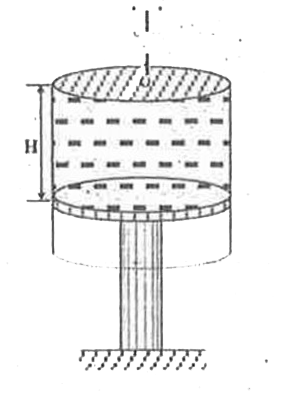
View Solution
Artificial satellites go round the earth in their respective orbits. Astronauts are able to float in side the satellite. Inside space of the satellite could be treated as gravity free space. If a beaker filled with a liquid upto height h having a small hole in the bottom is placed in such a satellite, you will wonder te liquid does not come out of the hole. You have to squeeze or force the liquid to come out. suppose a constant pressure p is applied on the liquid through piston to force it out through the hole. Out side pressure could be neglected in comparison with p Cross-sectional area of beaker is too greater than that of hole (A>>a)
View SolutionA liquid is filled in a spherical container of radius R up to a height h. At this position the liquid surface at the end is also horizontal. The contact angle is

View Solution
