If , then the function is (a) Increasing (b) Decreasing (c) Neither increasing nor decreasing (d) None of these
increasing
Decreasing
Neither increasing nor decreasing
None of these
The correct Answer is:B
To determine whether the function f(x)=xsinx+cosx+cos2x is increasing or decreasing in the interval (0,π2), we will follow these steps:
Step 1: Find the derivative of the function
We need to compute the derivative f′(x) to analyze the monotonicity of the function.
f′(x)=ddx(xsinx)+ddx(cosx)+ddx(cos2x)
Using the product rule on xsinx and the chain rule on cos2x:
1. Derivative of xsinx:
ddx(xsinx)=xcosx+sinx
2. Derivative of cosx:
ddx(cosx)=−sinx
3. Derivative of cos2x using the chain rule:
ddx(cos2x)=2cosx(−sinx)=−2sinxcosx
Combining these results:
f′(x)=(xcosx+sinx)−sinx−2sinxcosx
Step 2: Simplify the derivative
Now, we simplify f′(x):
f′(x)=xcosx+sinx−sinx−2sinxcosx
f′(x)=xcosx−2sinxcosx
f′(x)=cosx(x−2sinx)
Step 3: Analyze the sign of f′(x)
To determine where f′(x) is positive or negative, we need to analyze cosx and (x−2sinx) in the interval (0,π2).
1. cosx is positive in the interval (0,π2).
2. We need to check the sign of (x−2sinx).
Step 4: Check the inequality x<2sinx
We will check if x<2sinx for x∈(0,π2).
- At x=0:
0<2sin(0)(true)
- At x=π2:
π2<2sin(π2)=2(false)
To find where x=2sinx, we can analyze the function g(x)=2sinx−x. We can see that g(0)>0 and g(π2)<0, indicating that there is a root in (0,π2).
Conclusion
Since f′(x)<0 in the interval (0,π2), the function f(x) is decreasing in this interval.
Thus, the answer is:
(b) Decreasing
We need to compute the derivative f′(x) to analyze the monotonicity of the function.
ddx(xsinx)=xcosx+sinx
ddx(cosx)=−sinx
ddx(cos2x)=2cosx(−sinx)=−2sinxcosx
f′(x)=(xcosx+sinx)−sinx−2sinxcosx
Now, we simplify f′(x):
f′(x)=xcosx−2sinxcosx
f′(x)=cosx(x−2sinx)
To determine where f′(x) is positive or negative, we need to analyze cosx and (x−2sinx) in the interval (0,π2).
2. We need to check the sign of (x−2sinx).
We will check if x<2sinx for x∈(0,π2).
0<2sin(0)(true)
π2<2sin(π2)=2(false)
Since f′(x)<0 in the interval (0,π2), the function f(x) is decreasing in this interval.
(b) Decreasing
Topper's Solved these Questions
- BOOK - CENGAGE ENGLISHCHAPTER - MONOTONOCITY AND NAXINA-MINIMA OF FUNCTIONSEXERCISE - Multiple Correct Answer Type10videos
MONOTONOCITY AND NAXINA-MINIMA OF FUNCTIONS
- BOOK - CENGAGE ENGLISHCHAPTER - MONOTONOCITY AND NAXINA-MINIMA OF FUNCTIONSEXERCISE - Comprehension Type6videos
MONOTONOCITY AND NAXINA-MINIMA OF FUNCTIONS
- BOOK - CENGAGE ENGLISHCHAPTER - MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSEXERCISE - Matrix Match Type14videos
MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONS
- BOOK - CENGAGE ENGLISHCHAPTER - PAIR OF STRAIGHT LINESEXERCISE - Numberical Value Type5videos
PAIR OF STRAIGHT LINES
Similar Questions
The function f(x)=x1+|x| is (a) strictly increasing (b) strictly decreasing (c) neither increasing nor decreasing (d) none of these
View SolutionThe function f(x)=asinx+bcosxcsinx+dcosx is decreasing, if
View SolutionShow that f(x)=11+x2 is neither increasing nor decreasing on R .
View SolutionShow that f(x)=sinx is increasing on (0, π/2) and decreasing on (π/2, π) and neither increasing nor decreasing in (0, π) .
View SolutionFind the intervals in which function f(x) = sinx−cosx,0<x<2π is (i) increasing, (ii) decreasing.
View SolutionFind the intervals in which function f(x) = sinx−cosx,0<x<2π is (i) increasing, (ii) decreasing.
View SolutionFind the intervals in which f(x) = sin 3x, x∈[0,π2] is (i) increasing, (ii) decreasing.
View SolutionProve that the function given by f(x)=cosxis(a) strictly decreasing in (0,π)(b) strictly increasing in (π,2π), and(c) neither increasing nor decreasing in (0,2π)
View SolutionShow that f(x)=cosx is decreasing function on (0,π), increasing in (−π,0) and neither increasing nor decreasing in (−π,π).
View SolutionFor each of the following graphs, comment whether f(x) is increasing or decreasing or neither increasing nor decreasing at x = a.
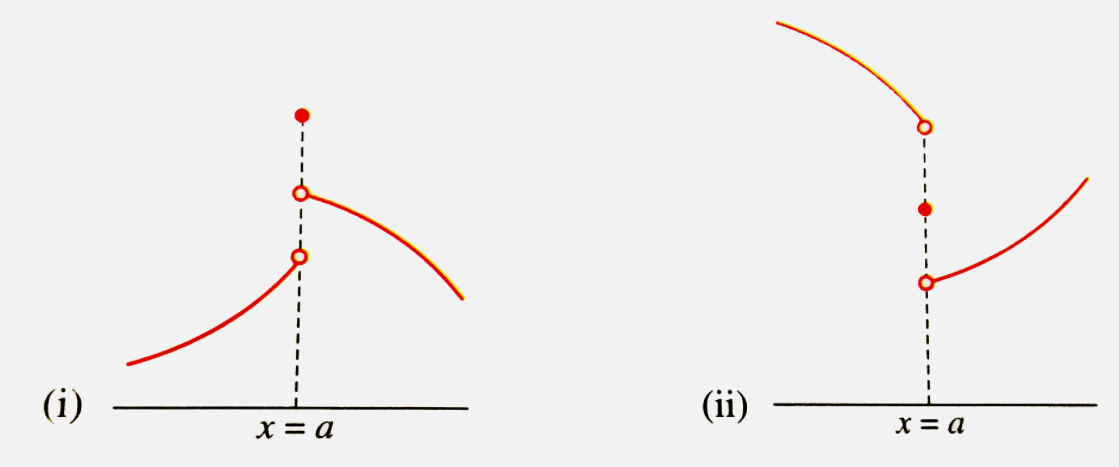
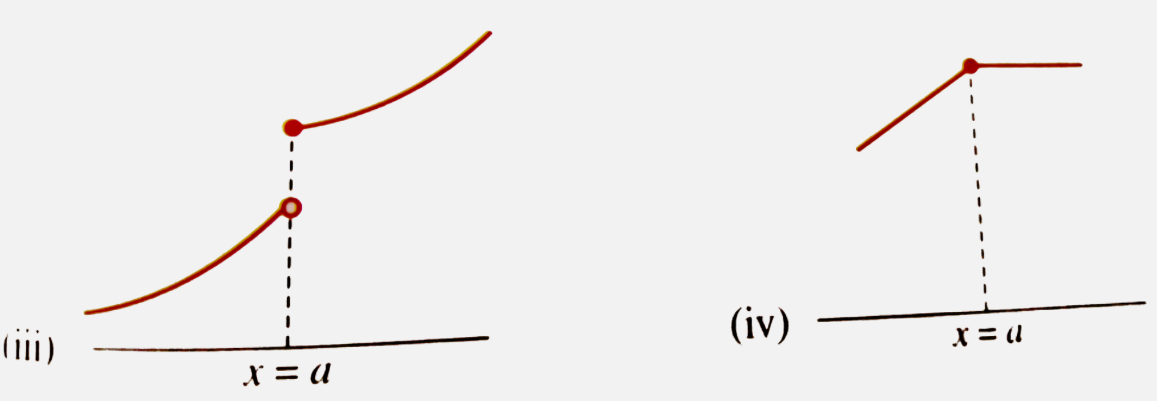 View Solution
View Solution

