How many ciritcal points functionf(x)=(x-1)|x-3|-4x+12 has? How many of these are points of local extrema?
To solve the problem, we need to analyze the function f(x)=(x−1)|x−3|−4x+12 to find its critical points and determine how many of these points are local extrema.
Step 1: Identify the piecewise nature of the function
The function contains an absolute value, |x−3|, which means we need to consider two cases based on the value of x:
1. Case 1: x<3
- Here, |x−3|=3−x.
- Therefore, the function becomes:
f(x)=(x−1)(3−x)−4x+12
2. Case 2: x≥3
- Here, |x−3|=x−3.
- Therefore, the function becomes:
f(x)=(x−1)(x−3)−4x+12
Step 2: Simplify the function for both cases
For Case 1 (x<3):
f(x)=(x−1)(3−x)−4x+12
=(3x−x2−3+x)−4x+12
=−x2+4x+9
For Case 2 (x≥3):
f(x)=(x−1)(x−3)−4x+12
=(x2−4x+3)−4x+12
=x2−8x+15
Step 3: Differentiate the function for both cases
For Case 1 (x<3):
f′(x)=−2x+4
For Case 2 (x≥3):
f′(x)=2x−8
Step 4: Find critical points by setting the derivative to zero
For Case 1 (x<3):
−2x+4=0⟹2x=4⟹x=2
For Case 2 (x≥3):
2x−8=0⟹2x=8⟹x=4
Step 5: Identify the critical points
The critical points we found are:
- x=2 (from Case 1)
- x=4 (from Case 2)
Step 6: Determine local extrema
To determine if these critical points are local extrema, we can check the second derivative or analyze the sign of the first derivative around these points.
For Case 1 (x<3):
- f′(x)=−2x+4
- f′′(x)=−2 (which is negative, indicating a local maximum)
For Case 2 (x≥3):
- f′(x)=2x−8
- f′′(x)=2 (which is positive, indicating a local minimum)
Conclusion
- The function has two critical points: x=2 and x=4.
- The critical point at x=2 is a local maximum, and the critical point at x=4 is a local minimum.
Final Answers
- Number of critical points: 2
- Number of local extrema: 2 (one maximum and one minimum)
The function contains an absolute value, |x−3|, which means we need to consider two cases based on the value of x:
- Here, |x−3|=3−x.
- Therefore, the function becomes:
f(x)=(x−1)(3−x)−4x+12
- Here, |x−3|=x−3.
- Therefore, the function becomes:
f(x)=(x−1)(x−3)−4x+12
f(x)=(x−1)(3−x)−4x+12
=(3x−x2−3+x)−4x+12
=−x2+4x+9
f(x)=(x−1)(x−3)−4x+12
=(x2−4x+3)−4x+12
=x2−8x+15
f′(x)=−2x+4
f′(x)=2x−8
−2x+4=0⟹2x=4⟹x=2
2x−8=0⟹2x=8⟹x=4
The critical points we found are:
- x=2 (from Case 1)
- x=4 (from Case 2)
To determine if these critical points are local extrema, we can check the second derivative or analyze the sign of the first derivative around these points.
- f′(x)=−2x+4
- f′′(x)=−2 (which is negative, indicating a local maximum)
- f′(x)=2x−8
- f′′(x)=2 (which is positive, indicating a local minimum)
- The function has two critical points: x=2 and x=4.
- The critical point at x=2 is a local maximum, and the critical point at x=4 is a local minimum.
- Number of critical points: 2
- Number of local extrema: 2 (one maximum and one minimum)
Topper's Solved these Questions
- BOOK - CENGAGE ENGLISHCHAPTER - MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSEXERCISE - Solved Examples20videos
MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONS
- BOOK - CENGAGE ENGLISHCHAPTER - MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSEXERCISE - Concept Application Exercise 6.110videos
MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONS
- BOOK - CENGAGE ENGLISHCHAPTER - METHODS OF DIFFERENTIATIONEXERCISE - Single Correct Answer Type46videos
METHODS OF DIFFERENTIATION
- BOOK - CENGAGE ENGLISHCHAPTER - MONOTONOCITY AND NAXINA-MINIMA OF FUNCTIONSEXERCISE - Comprehension Type6videos
MONOTONOCITY AND NAXINA-MINIMA OF FUNCTIONS
Similar Questions
The smallest positive integral value of a, such that the function f(x)=x4−4ax2+10 has more two local extrema, is
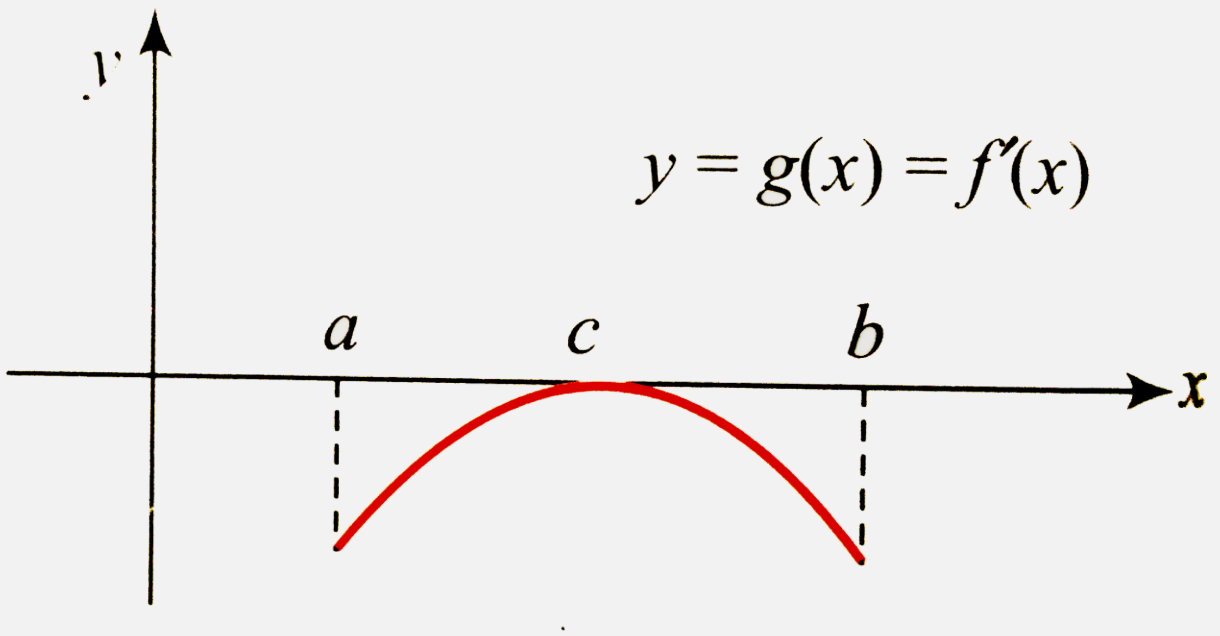
View SolutionFollowing is the graph of y = f' (x) , given that f(c) = 0. Analyse the graph and answer the following questions.
(a) How many times the graph of y = f(x) will intersect the x - axis?
(b) Discuss the type of roots of the equation f (x) = 0, a≤x≤b.
(c) How many points of inflection the graph of y=f(x),a≤x≤b, has?
(d) Find the points of local maxima/minima ofy=f(x),a<xb.
(e) How many roots equation f''(x)=0 has?
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
|2x−1|=4x+5 has how many numbers in its solution set ?
A0B1C2Dan infinite number - Question 2 - Select One
How many solutions exist to the equation |x|=|2x−1|?
A0B1C2D3
How many permutations can be there with x3.y2z4? How many of these arrangements, all z are not together?
View SolutionDiscuss the extremum of the function f(x)=(x-1)(x-2)(x-3).How many criticla points f(x) has?
View SolutionFind the points at which the function f given by f(x)=(x−2)4(x+1)3 has local maxima local minima point of inflexion
View SolutionFind the points at which the function f given by f(x)=(x−2)4(x+1)3 has local maxima and local minima and points of inflexion.
View SolutionFind the points of local maxima, local minima and the points of inflection of the function f(x)=x5−5x4+5x3−1 . Also, find the corresponding local maximum and local minimum values
View SolutionFind the points of local maxima, local minima and the points of inflection of the function f(x)=x5−5x4+5x3−1. Also, find the corresponding local maximum and local minimum values.
View Solution

