Discuss the extrema of the following functions
(i)f(x)=|x|,(ii)f(x)=e−|x|,(iii)f(x)=x2/3
To discuss the extrema of the given functions, we will analyze each function step by step.
(i) Function: f(x)=|x|
1. Understanding the Function:
- The function f(x)=|x| represents the absolute value of x.
- It is defined as:
f(x)={xif x≥0−xif x<0
2. Finding Critical Points:
- The function is continuous everywhere, but it is not differentiable at x=0.
- We can find the derivative:
f′(x)={1if x>0−1if x<0
- At x=0, the derivative does not exist.
3. Analyzing Extrema:
- The function has a minimum at x=0 where f(0)=0.
- As x→∞ or x→−∞, f(x)→∞.
- Therefore, there is no maximum value.
Conclusion for (i):
- Minimum: f(0)=0 at x=0
- Maximum: None (approaches infinity)
(ii) Function: f(x)=e−|x|
1. Understanding the Function:
- The function f(x)=e−|x| is always positive and decreases as |x| increases.
2. Finding Critical Points:
- The function is continuous and differentiable everywhere.
- The derivative is:
f′(x)={−e−xif x>0exif x<0
- Setting f′(x)=0 gives no critical points since e−x and ex are never zero.
3. Analyzing Extrema:
- The maximum occurs at x=0 where f(0)=e0=1.
- As x→±∞, f(x)→0.
Conclusion for (ii):
- Minimum: None (approaches 0)
- Maximum: f(0)=1 at x=0
(iii) Function: f(x)=x2/3
1. Understanding the Function:
- The function f(x)=x2/3 is defined for all real x.
2. Finding Critical Points:
- The derivative is:
f′(x)=23x−1/3
- Setting f′(x)=0 gives x=0 as the only critical point.
3. Analyzing Extrema:
- At x=0, f(0)=0.
- As x→∞ or x→−∞, f(x)→∞.
Conclusion for (iii):
- Minimum: f(0)=0 at x=0
- Maximum: None (approaches infinity)
Summary of Extrema
1. For f(x)=|x|:
- Minimum: 0 at x=0
- Maximum: None
2. For f(x)=e−|x|:
- Minimum: None (approaches 0)
- Maximum: 1 at x=0
3. For f(x)=x2/3:
- Minimum: 0 at x=0
- Maximum: None
- The function f(x)=|x| represents the absolute value of x.
- It is defined as:
f(x)={xif x≥0−xif x<0
- The function is continuous everywhere, but it is not differentiable at x=0.
- We can find the derivative:
f′(x)={1if x>0−1if x<0
- At x=0, the derivative does not exist.
- The function has a minimum at x=0 where f(0)=0.
- As x→∞ or x→−∞, f(x)→∞.
- Therefore, there is no maximum value.
- Minimum: f(0)=0 at x=0
- Maximum: None (approaches infinity)
- The function f(x)=e−|x| is always positive and decreases as |x| increases.
- The function is continuous and differentiable everywhere.
- The derivative is:
f′(x)={−e−xif x>0exif x<0
- Setting f′(x)=0 gives no critical points since e−x and ex are never zero.
- The maximum occurs at x=0 where f(0)=e0=1.
- As x→±∞, f(x)→0.
- Minimum: None (approaches 0)
- Maximum: f(0)=1 at x=0
- The function f(x)=x2/3 is defined for all real x.
- The derivative is:
f′(x)=23x−1/3
- Setting f′(x)=0 gives x=0 as the only critical point.
- At x=0, f(0)=0.
- As x→∞ or x→−∞, f(x)→∞.
- Minimum: f(0)=0 at x=0
- Maximum: None (approaches infinity)
1. For f(x)=|x|:
- Minimum: 0 at x=0
- Maximum: None
- Minimum: None (approaches 0)
- Maximum: 1 at x=0
- Minimum: 0 at x=0
- Maximum: None
Topper's Solved these Questions
- BOOK - CENGAGE ENGLISHCHAPTER - MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSEXERCISE - Solved Examples20videos
MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONS
- BOOK - CENGAGE ENGLISHCHAPTER - MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSEXERCISE - Concept Application Exercise 6.110videos
MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONS
- BOOK - CENGAGE ENGLISHCHAPTER - METHODS OF DIFFERENTIATIONEXERCISE - Single Correct Answer Type46videos
METHODS OF DIFFERENTIATION
- BOOK - CENGAGE ENGLISHCHAPTER - MONOTONOCITY AND NAXINA-MINIMA OF FUNCTIONSEXERCISE - Comprehension Type6videos
MONOTONOCITY AND NAXINA-MINIMA OF FUNCTIONS
Similar Questions
Let A={x:−1≤x≤1}=B be a function f:A→B. Then find the nature of each of the following functions.
(i) f(x)=|x| (ii) f(x)=x|x|
(iii) f(x)=x3 (iv) f(x)=sinπx2View SolutionFind the period of the following functions
(i) f(x)=|sin3x|
(ii) f(x)=2cosec(5x−6)+7
(iii) f(x)=x−[x−2.6], where [.] represents the greatest integer function.View SolutionConsider the following function f, whose graph is given below.
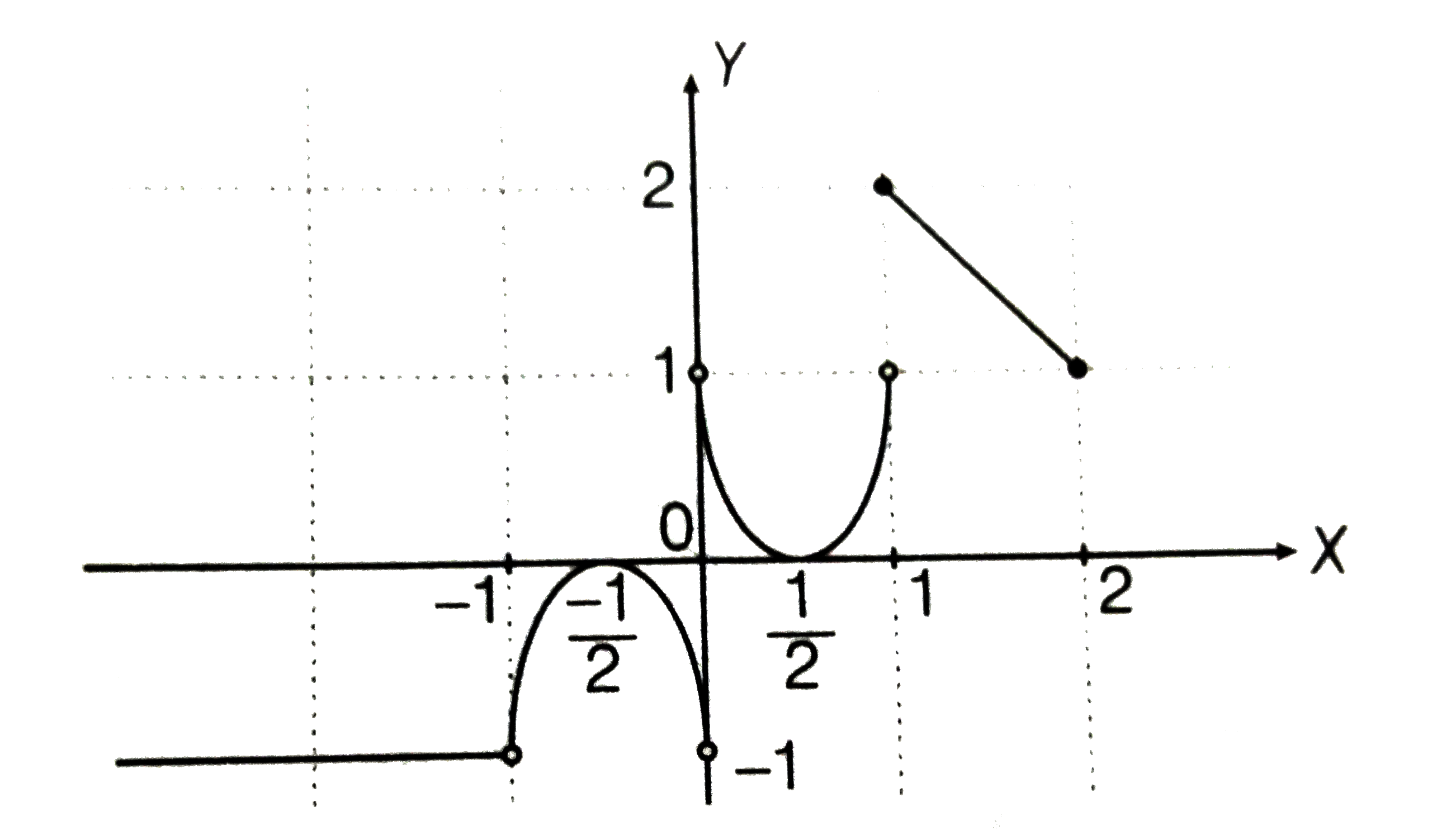
Draw the graph of the following functions.
(i) |f(x)|
(ii) f(|x|)
(iii) |f(|x|)−1|View SolutionFind the domain and range of the following functions.
(i) f(x)=√2x−3 (ii) f(x)=1x−2
(iii) f(x)=x2+3 (iv) f(x)=1x2+2View SolutionFind the range of each of the following functions: f(x)=|x−3| f(x)=1−|x−2| f(x)=|x−4|x−4
View SolutionFind the range of each of the following functions: f(x)=1√x−5 (ii) f(x)=√6−x2 (iii) f(x)=x1−x2 (iv) f(x)=32−x2
View SolutionFind the range of the following functions given by
f(x)=32−x2 (ii) f(x)=1−|x−2|
(iii) f(x)=|x−3| (iv) f(x)=1+3cos2xView SolutionFind the the domain of following functions:
(i) f(x)=√x2−5 (ii) sin(x3−x)View SolutionFind the domain and range of the following real functions:(i) f(x)=−|x| (ii) f(x)=√9−x2
View SolutionFind the inverse of the following function. (i) f(x)=sin−1(x3),x∈[−3,3] (ii) f(x)=5logex,x>0 (iii) f(x)=loge(x+√x2+1)
View Solution

