The lateral edge of a regular hexagonal pyramid is 1cm. If the volume is maximum, then find its height.

x2+h2=1
volume ,V=13×6×√34x2h=√32h(1−h2)
for v(h)=1√3 or Vmax=(1/3)
Topper's Solved these Questions
- BOOK - CENGAGE ENGLISHCHAPTER - MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSEXERCISE - Solved Examples20videos
MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONS
- BOOK - CENGAGE ENGLISHCHAPTER - MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSEXERCISE - Concept Application Exercise 6.110videos
MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONS
- BOOK - CENGAGE ENGLISHCHAPTER - METHODS OF DIFFERENTIATIONEXERCISE - Single Correct Answer Type46videos
METHODS OF DIFFERENTIATION
- BOOK - CENGAGE ENGLISHCHAPTER - MONOTONOCITY AND NAXINA-MINIMA OF FUNCTIONSEXERCISE - Comprehension Type6videos
MONOTONOCITY AND NAXINA-MINIMA OF FUNCTIONS
Similar Questions
The lateral edge of a regular rectangular pyramid is acmlong. The lateral edge makes an angle α with the plane of the base. Find the value of α for which the volume of the pyramid is greatest.
View SolutionA cone is inscribed in a sphere of radius 12 cm. If the volume of the cone is maximum, find its height.
View Solution
Knowledge Check
- Question 1 - Select One
Find the volume of a rectangle hexagonal pyramid with a base of side length 4 and a height of 9.
A12√3B36√3C72√3D144√3
The perimeter of a regular hexagon is 18 cm. How long is its oneside?
View SolutionThe height of a cone is 15cm. If its volume is 500π cm3 , then find the radius of its base.
View SolutionSix negative equal charge are placed at the vertical of a regular hexagon . 6q charge is placed at the centre of the hexagon . Find the electric dipole moment of the system.
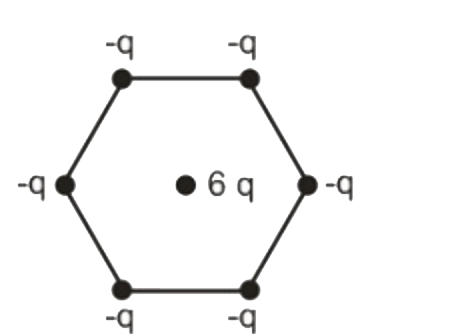 View Solution
View SolutionIf center of a regular hexagon is at the origin and one of the vertices on the Argand diagram is 1+2i , then its perimeter is 2√5 b. 6√2 c. 4√5 d. 6√5
View SolutionFind the perimeter of a regular hexagon with each side measuring 8 m.
View SolutionFind the perimeter of a regular hexagon with each side measuring 8 m.
View SolutionFind the area of the following regular hexagon Figure
View Solution

