A right triangle is drawn in a semicircle of radius 12 with one of its legs along the diameter. If the maximum area of the triangle is M , then the value of 32√3Mc is______
The correct Answer is:9
BC×Ce=AC×CD
therfore(BC)(CE)=x(1−x)
But BC=CE
thereBC=√x(1−x)
∴Area△=x√x−x22
or △=x3−x44
or d△2dx=3x2−4x34
If d△2dx=0 then x=34 which is the point of maxima
Hence maximum area is 3√332

Topper's Solved these Questions
- BOOK - CENGAGE ENGLISHCHAPTER - MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSEXERCISE - Single Correct Answer Type13videos
MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONS
- BOOK - CENGAGE ENGLISHCHAPTER - MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSEXERCISE - Linked comprehension Type2videos
MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONS
- BOOK - CENGAGE ENGLISHCHAPTER - MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSEXERCISE - Multiple correct answers type48videos
MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONS
- BOOK - CENGAGE ENGLISHCHAPTER - METHODS OF DIFFERENTIATIONEXERCISE - Single Correct Answer Type46videos
METHODS OF DIFFERENTIATION
- BOOK - CENGAGE ENGLISHCHAPTER - MONOTONOCITY AND NAXINA-MINIMA OF FUNCTIONSEXERCISE - Comprehension Type6videos
MONOTONOCITY AND NAXINA-MINIMA OF FUNCTIONS
Similar Questions
An equilateral triangle is drawn on a diagonal of a square of perimeter 16cm. If the area of triangle is x√3cm2, then the value of x is
View SolutionA small card is in the shape of an isosceles triangle with a semicircle on its base. If the diameter of the semicircle is 6 cm, and the hright of the triangle is 3 cm, find the area of the card.
View Solution
Knowledge Check
- Question 1 - Select One
A right triangle , shown below , has a longer leg measing 16√3 centimeters . How long is the hypotenuse of the triangle , in centimeters ?
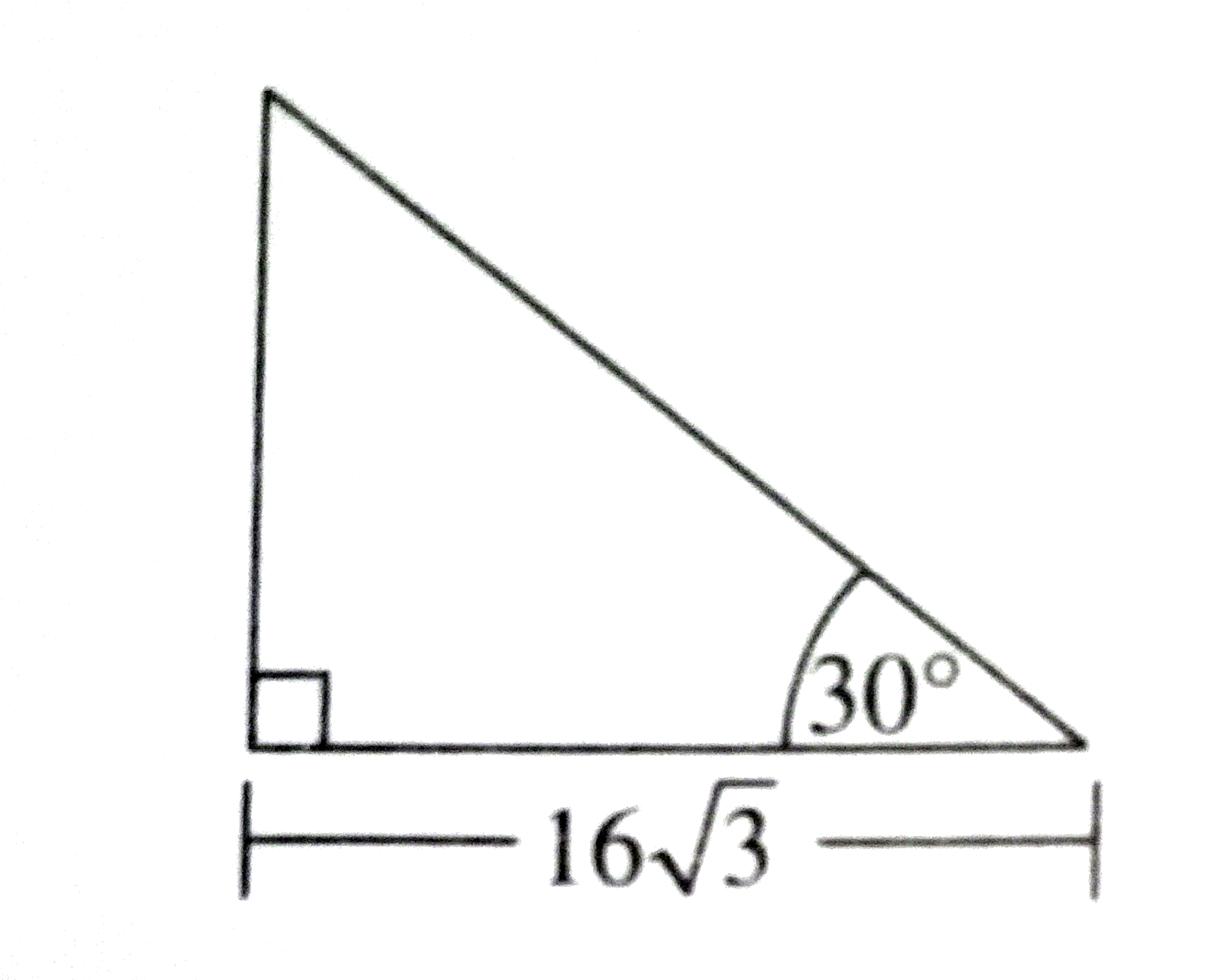 A8B8√2C16D32
A8B8√2C16D32
The area of a right triangle is 6864 sq. units. If the ratio of its legs is 143:24, then the value of r is ______
View SolutionThe three sides of a trapezium are equal each being 6 cms long. Let Δcm2 be the maximum area of the trapezium. The value of √3Δ is :
View SolutionIn a ΔABC, a semicircle is inscribed, whose diameter lies on the side c. Then the radius of the semicircle is (Where Δ is the area of the triangle ABC)
View SolutionConsider a right triangle with legs of length a and b and hypotenuse of lengthc. If k denotes the area of the triangle then the value of (a+b) equals
View SolutionThe base and the height of a triangle are in the ratio 5:3. If the area of the triangle is 67.5 m2, find its base and height.
View SolutionThe lengths of the two shorter legs of a right triangle add up to 40 units. What is the maximum possible area of the triangle?
View SolutionIn the right triangle BAC,∠A=π2anda+b=8. The area of the triangle is maximum when ∠C , is
View Solution

