Given the continuous fuunction
y=f(x)=⎧⎪⎨⎪⎩x2+10x+8x≤−2ax2+bx+c−2<x<0,a≠0x2+2xx≥0
if a line L touches the graph of y=f(x) at three points , then
if y= f(x) is differentiable at x=0, then the value of B
is -1
is 2
is 4
connot be determined
The correct Answer is:B
To solve the problem step by step, we need to ensure that the function f(x) is continuous and differentiable at x=0. We will analyze the function piecewise and find the necessary conditions.
Step 1: Define the function piecewise
The function f(x) is defined as follows:
- For x≤−2: f(x)=x2+10x+8
- For −2<x<0: f(x)=ax2+bx+c
- For x≥0: f(x)=x2+2x
Step 2: Ensure continuity at x=−2
To ensure continuity at x=−2, we need:
limx→−2−f(x)=limx→−2+f(x)
Calculating the left-hand limit:
f(−2)=(−2)2+10(−2)+8=4−20+8=−8
Now for the right-hand limit:
f(−2)=a(−2)2+b(−2)+c=4a−2b+c
Setting these equal for continuity:
4a−2b+c=−8(1)
Step 3: Ensure continuity at x=0
Next, we ensure continuity at x=0:
limx→0−f(x)=limx→0+f(x)
Calculating the left-hand limit:
f(0)=a(0)2+b(0)+c=c
Now for the right-hand limit:
f(0)=(0)2+2(0)=0
Setting these equal for continuity:
c=0(2)
Step 4: Substitute c back into equation (1)
Substituting c=0 into equation (1):
4a−2b+0=−8
This simplifies to:
4a−2b=−8(3)
Step 5: Ensure differentiability at x=0
For differentiability at x=0, the left-hand derivative must equal the right-hand derivative:
limx→0−f′(x)=limx→0+f′(x)
Calculating the left-hand derivative:
f′(x)=2ax+b⇒limx→0−f′(x)=b
Calculating the right-hand derivative:
f′(x)=2x+2⇒limx→0+f′(x)=2
Setting these equal for differentiability:
b=2(4)
Step 6: Solve for a using equation (3)
Substituting b=2 into equation (3):
4a−2(2)=−8
This simplifies to:
4a−4=−8
Adding 4 to both sides:
4a=−4
Dividing by 4:
a=−1
Final Result
The value of b is:
2
The function f(x) is defined as follows:
- For x≤−2: f(x)=x2+10x+8
- For −2<x<0: f(x)=ax2+bx+c
- For x≥0: f(x)=x2+2x
To ensure continuity at x=−2, we need:
limx→−2−f(x)=limx→−2+f(x)
Calculating the left-hand limit:
f(−2)=(−2)2+10(−2)+8=4−20+8=−8
Now for the right-hand limit:
f(−2)=a(−2)2+b(−2)+c=4a−2b+c
Setting these equal for continuity:
4a−2b+c=−8(1)
Next, we ensure continuity at x=0:
limx→0−f(x)=limx→0+f(x)
Calculating the left-hand limit:
f(0)=a(0)2+b(0)+c=c
Now for the right-hand limit:
f(0)=(0)2+2(0)=0
Setting these equal for continuity:
c=0(2)
Substituting c=0 into equation (1):
4a−2b+0=−8
This simplifies to:
4a−2b=−8(3)
For differentiability at x=0, the left-hand derivative must equal the right-hand derivative:
limx→0−f′(x)=limx→0+f′(x)
Calculating the left-hand derivative:
f′(x)=2ax+b⇒limx→0−f′(x)=b
Calculating the right-hand derivative:
f′(x)=2x+2⇒limx→0+f′(x)=2
Setting these equal for differentiability:
b=2(4)
Substituting b=2 into equation (3):
4a−2(2)=−8
This simplifies to:
4a−4=−8
Adding 4 to both sides:
4a=−4
Dividing by 4:
a=−1
The value of b is:
2
Similar Questions
Knowledge Check
If f(x)=ax2+bx+c,a≠0 and a, b , and c are all negative , which could be the graph of f(x) ?
A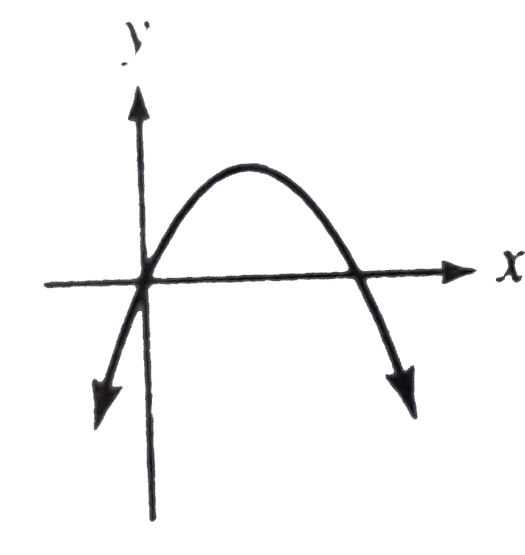 B
B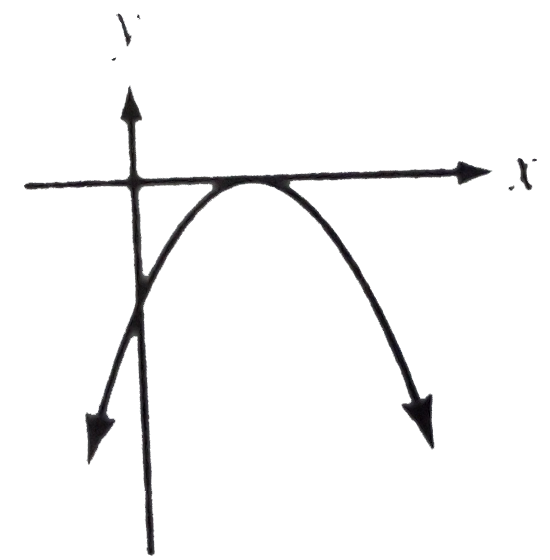 C
C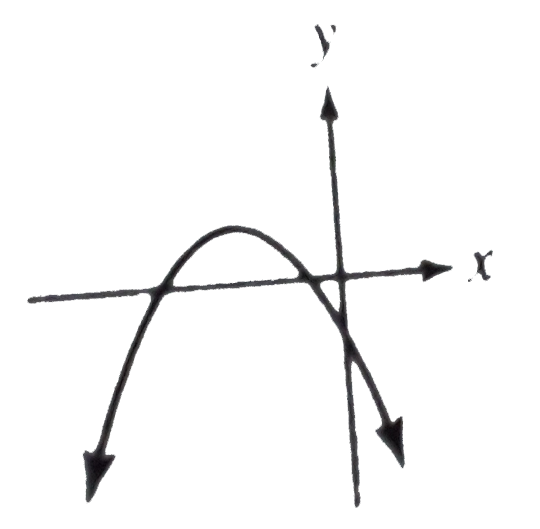 D
D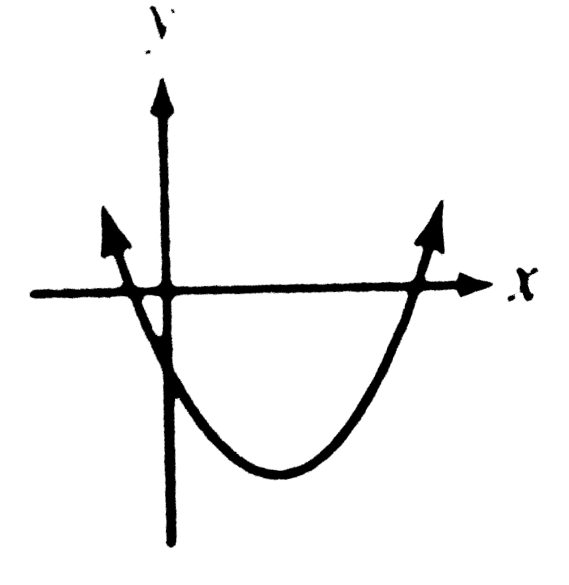
Show that the function f given by f(x)={x2+5ifx≠03ifx=0 is not continuous at x=0
View SolutionLet f(x)=ax2−bx+c2,b≠0andf(x)≠0 for all x∈R. Then
View SolutionDiscuss the continuity of f(x)={sin22xx2, x≠01, x=0,at x=0.
View Solutioniff(x)={8x−4x−2x+1x2x>0x2x≤0
is continuous at x=0 , then the value of λ is
View SolutionGiven the graph of y=f(x).

Draw the graphs of the followin.
(a) y=f(1−x) (b) y=−2f(x)
(c) y=f(2x) (d) y=1−f(x)
View SolutionLet y=f(x)={e1x2ifx≠00ifx=0 then which of the following can best represent the graph of y=f(x)?
View Solution2x+y≤6,x+2y≤8,x≥0,y≥0
View Solution
