A beam is supported at the two ends and is uniformly loaded. The bending moment M at a distance x from one end is given by M=WL2x−W2x2 M=Wx3−W3x3L2 Find the point at which M is maximum in each case.
To find the point at which the bending moment M is maximum for the given equations, we will follow these steps for each case.
Case 1:
Given the bending moment equation:
M=WL2x−W2x2
Step 1: Find the first derivative of M with respect to x
To find the maximum, we first need to take the derivative of M:
dMdx=WL2−Wx
Step 2: Set the first derivative equal to zero
To find the critical points, we set the first derivative equal to zero:
WL2−Wx=0
Step 3: Solve for x
Rearranging gives:
Wx=WL2
x=L2
Step 4: Verify if this point is a maximum using the second derivative test
Now, we find the second derivative of M:
d2Mdx2=−W
Since −W<0, this confirms that x=L2 is indeed a maximum.
Conclusion for Case 1:
The bending moment M is maximum at:
x=L2
---
Case 2:
Given the bending moment equation:
M=Wx3−W3x3L2
Step 1: Find the first derivative of M with respect to x
Taking the derivative:
dMdx=W3−WL2x2
Step 2: Set the first derivative equal to zero
Setting the first derivative equal to zero:
W3−WL2x2=0
Step 3: Solve for x
Rearranging gives:
WL2x2=W3
x2=L23
x = \frac{L}{\sqrt{3}} \quad \text{(taking only the positive root since x must be positive)}
Step 4: Verify if this point is a maximum using the second derivative test
Now, we find the second derivative of M:
d2Mdx2=−2WL2
Since −2WL2<0, this confirms that x=L√3 is indeed a maximum.
Conclusion for Case 2:
The bending moment M is maximum at:
x=L√3
---
Summary of Results:
1. For the first case, M is maximum at x=L2.
2. For the second case, M is maximum at x=L√3.
---
Given the bending moment equation:
M=WL2x−W2x2
dMdx=WL2−Wx
WL2−Wx=0
Wx=WL2
x=L2
d2Mdx2=−W
Since −W<0, this confirms that x=L2 is indeed a maximum.
The bending moment M is maximum at:
x=L2
Given the bending moment equation:
M=Wx3−W3x3L2
dMdx=W3−WL2x2
W3−WL2x2=0
WL2x2=W3
x2=L23
x = \frac{L}{\sqrt{3}} \quad \text{(taking only the positive root since x must be positive)}
d2Mdx2=−2WL2
Since −2WL2<0, this confirms that x=L√3 is indeed a maximum.
The bending moment M is maximum at:
x=L√3
1. For the first case, M is maximum at x=L2.
2. For the second case, M is maximum at x=L√3.
Topper's Solved these Questions
Similar Questions
A beam is supported at the two ends and is uniformly loaded. The bending moment M at a distance x from one end is given by (i)M=WL2x−W2x2 (ii) M=Wx3−W3x3L2 Find the point at which M is maximum in each case.
View SolutionA beam is supported at the two ends and is uniformly loaded. The bending moment M at a distance x from one end is given by M=Wx3−W3x3L2 . Find the point at which M is maximum.
View SolutionA beam is supported at the two ends and is uniformly loaded. The bending moment M at a distance x from one end is given by M=WL2x−W2x2 . Find the point at which M is maximum.
View SolutionA beam of weight W supports a block of weight W. The length of the beam is L. and weight is at a distance L4 from the left end of the beam. The beam rests on two rigid supports at its ends. Find the reactions of the supports.

View SolutionThe maximum intensity in the case of n identical incoherent waves each of intensity 2Wm2 is n 32Wm2 the value of n is.
View SolutionA laser beam has intensity 2.5 x (1014)W(m−2). Find the amplitudes of electric and magnetic fields in the beam.
View SolutionIn Fig.1.35 a uniform bar of length l m is supported at its ends and loaded by a weight W kgf at its middle. In equilibrium find the reaction R1andR2 at the ends.
View Solution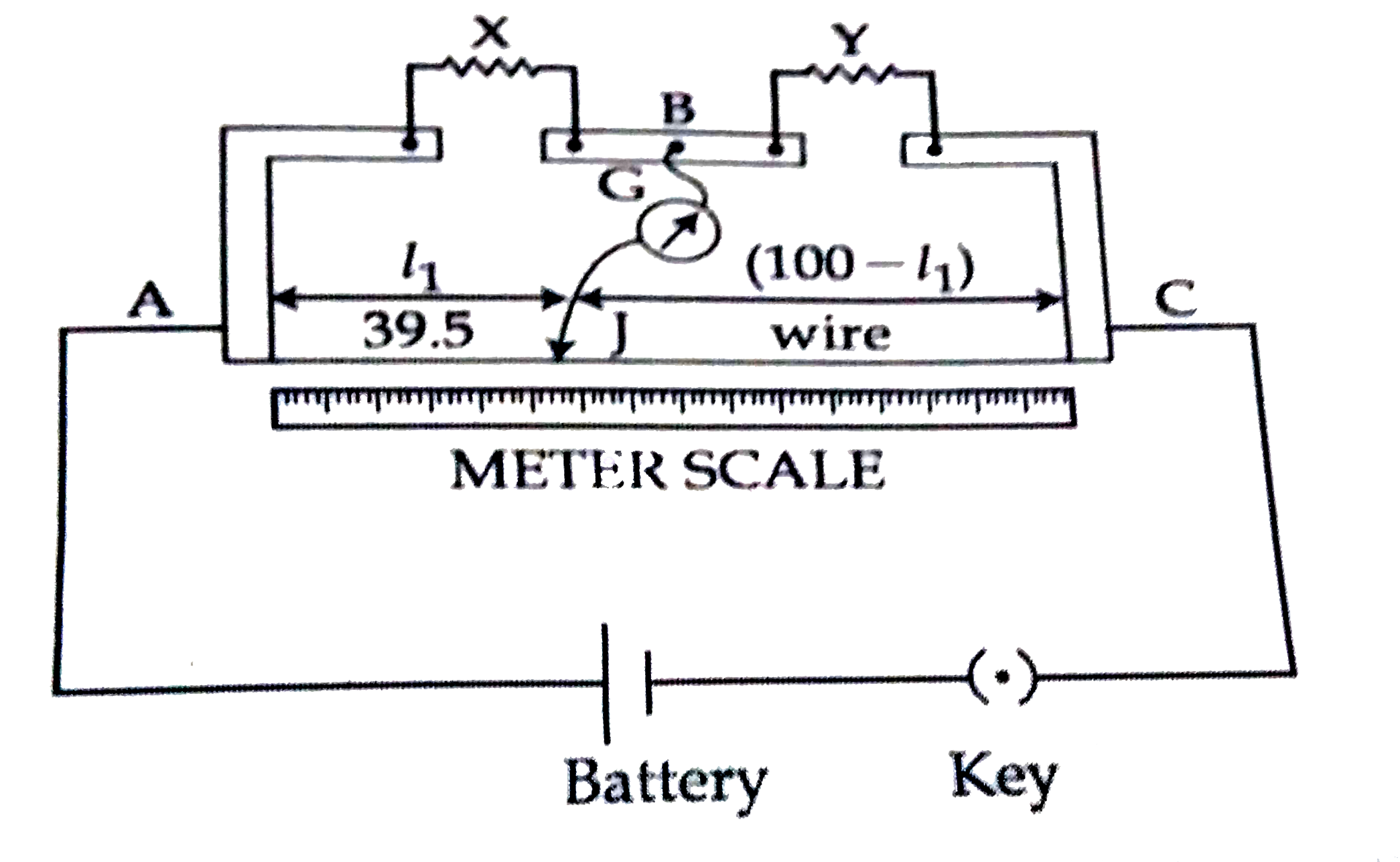
In a meter bridge, as shown in the figure, it is given that resistance Y=12.5Ω and that the balance is obtained at a distance 39.5cm from end A (by jockey J). After interchanging the resistance X and Y, a new balance point is found at a distance l2 from end A. What are the values of X and l2 ?
View Solution
The kinetic energy of a uniform rod of mass m rotating with constant angular velocit ω about one of its end which is fixed as shown in figure is mω2l2N find N
View SolutionA uniform rod mass m and length l is provided at one end and is rotated with constant angular velocity ω in a horizontal plane. Tension in the rod at a distance (√3l/2) from pivoted end is (Assume gravity free space)
View Solution
