In Fig. 6.11, OP, OQ, OR and OS are four rays. Prove that ∠POQ+∠QOR+∠SOR+∠POS=360o
To prove that ∠POQ+∠QOR+∠SOR+∠POS=360∘, we will follow these steps:
Step 1: Identify the rays and angles
We have four rays: OP, OQ, OR, and OS. The angles we need to consider are ∠POQ, ∠QOR, ∠SOR, and ∠POS.
Step 2: Extend ray OQ
Extend ray OQ in the opposite direction to point T. Now, TOQ is a straight line.
Step 3: Use the straight angle property
Since TOQ is a straight line, we know that:
∠TOP+∠POQ=180∘
This is our first equation.
Step 4: Consider the angles around point O
Now, consider the angles going in the opposite direction from point O:
∠TOS+∠SOQ=180∘
This is our second equation.
Step 5: Break down ∠SOQ
We can express ∠SOQ as the sum of two angles:
∠SOQ=∠SOR+∠QOR
Substituting this into our second equation gives:
∠TOS+∠SOR+∠QOR=180∘
Step 6: Add the two equations
Now, we add the two equations together:
1. ∠TOP+∠POQ=180∘
2. ∠TOS+∠SOR+∠QOR=180∘
Adding these gives:
∠TOP+∠POQ+∠TOS+∠SOR+∠QOR=360∘
Step 7: Combine angles
Notice that ∠TOP+∠TOS=∠POS. So we can rewrite the equation as:
∠POS+∠POQ+∠SOR+∠QOR=360∘
Conclusion
Thus, we have proved that:
∠POQ+∠QOR+∠SOR+∠POS=360∘
We have four rays: OP, OQ, OR, and OS. The angles we need to consider are ∠POQ, ∠QOR, ∠SOR, and ∠POS.
Extend ray OQ in the opposite direction to point T. Now, TOQ is a straight line.
Since TOQ is a straight line, we know that:
∠TOP+∠POQ=180∘
This is our first equation.
Now, consider the angles going in the opposite direction from point O:
∠TOS+∠SOQ=180∘
This is our second equation.
We can express ∠SOQ as the sum of two angles:
∠SOQ=∠SOR+∠QOR
Substituting this into our second equation gives:
∠TOS+∠SOR+∠QOR=180∘
Now, we add the two equations together:
1. ∠TOP+∠POQ=180∘
2. ∠TOS+∠SOR+∠QOR=180∘
∠TOP+∠POQ+∠TOS+∠SOR+∠QOR=360∘
Notice that ∠TOP+∠TOS=∠POS. So we can rewrite the equation as:
∠POS+∠POQ+∠SOR+∠QOR=360∘
Thus, we have proved that:
∠POQ+∠QOR+∠SOR+∠POS=360∘
Topper's Solved these Questions
Similar Questions
In Figure, OP, OQ, OR and OS are four rays. Prove that ∠POQ+ ∠QOR+ ∠SOR+ ∠POS=3600
View SolutionIn Fig 7.51, PR > PQand PS bisects ∠QPR. Prove that ∠PSR >∠PSQ.

View SolutionIn Fig. 6.15, ∠PQR=∠PRQ, then prove that ∠PQS=∠PRT.
View SolutionIn Fig. 10.101, PQ and PR are two tangents to a circle with centre O . If ∠QPR=46o , then ∠QOR equals (a) 67o (b) 134o (c) 44o (d) 46o
View SolutionIn figure, if PQ||RS, prove that ΔPOQΔSOR.
View SolutionIn Figure, PS=QR and ∠SPQ=∠RQP. Prove that PQS ≅ QPR, PR=QS and ∠QPR= ∠PQS
View SolutionIn Fig. 6.10, ray OS stands on a line POQ. Ray OR and ray OT are angle bisectors of ∠POS and ∠SOQ , respectively. If ∠POS=x , find ∠ROT .
View SolutionIn Fig. 6.17, POQ is a line. Ray OR is perpendicular to line PQ. OS is another ray lying between rays OP and OR. Prove that ∠ROS=12(∠QOS−∠POS).
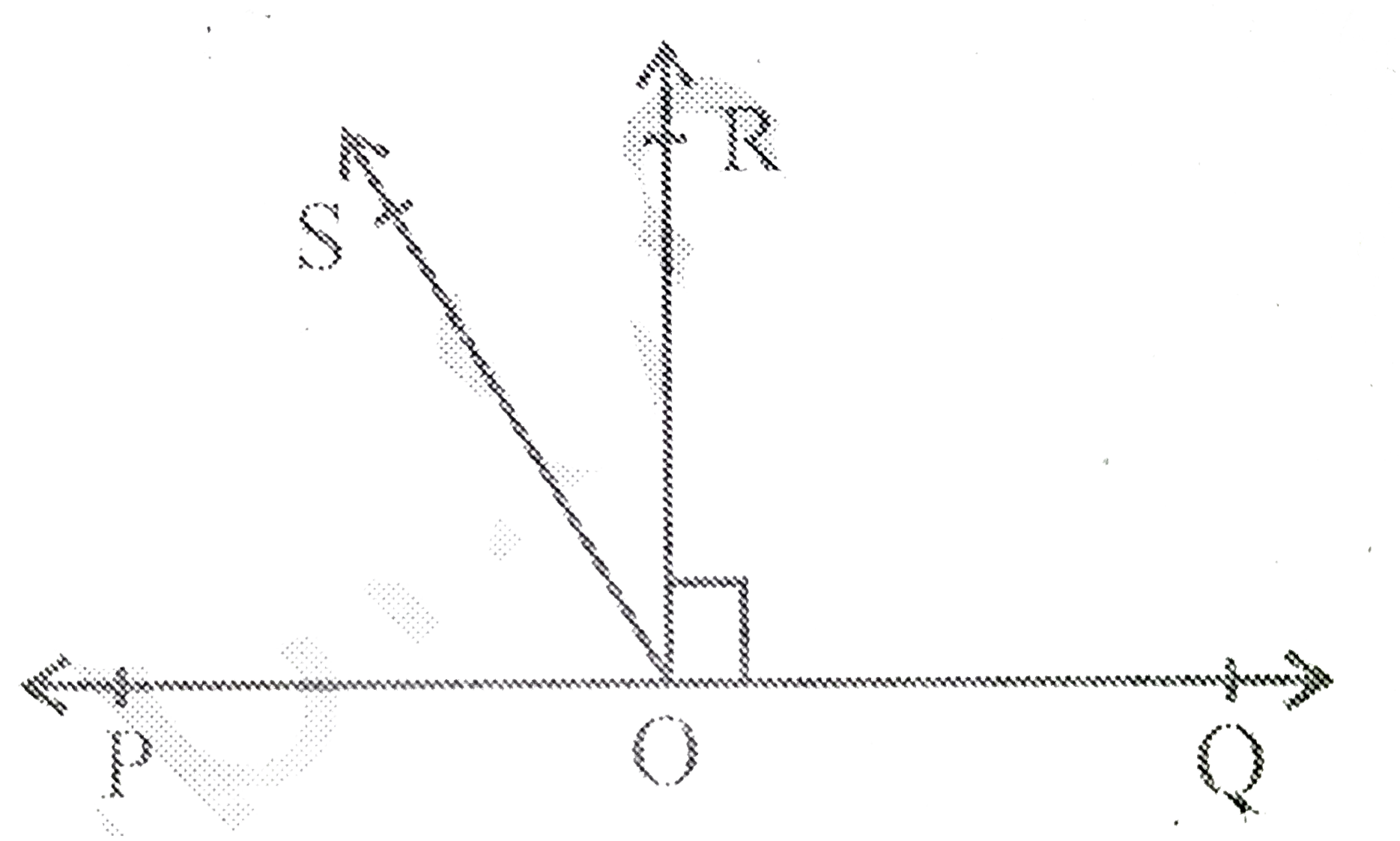
View SolutionIn Fig. 6.17, POQ is a line. Ray OR is perpendicular to line PQ. OS is another ray lying between rays OP and OR. Prove that ∠ROS=12(∠QOS−∠POS).
View SolutionIn Fig. , if QTPR=QRQS and ∠1=∠2 . Prove that PQS~TQR . (FIGURE)
View Solution
