Question

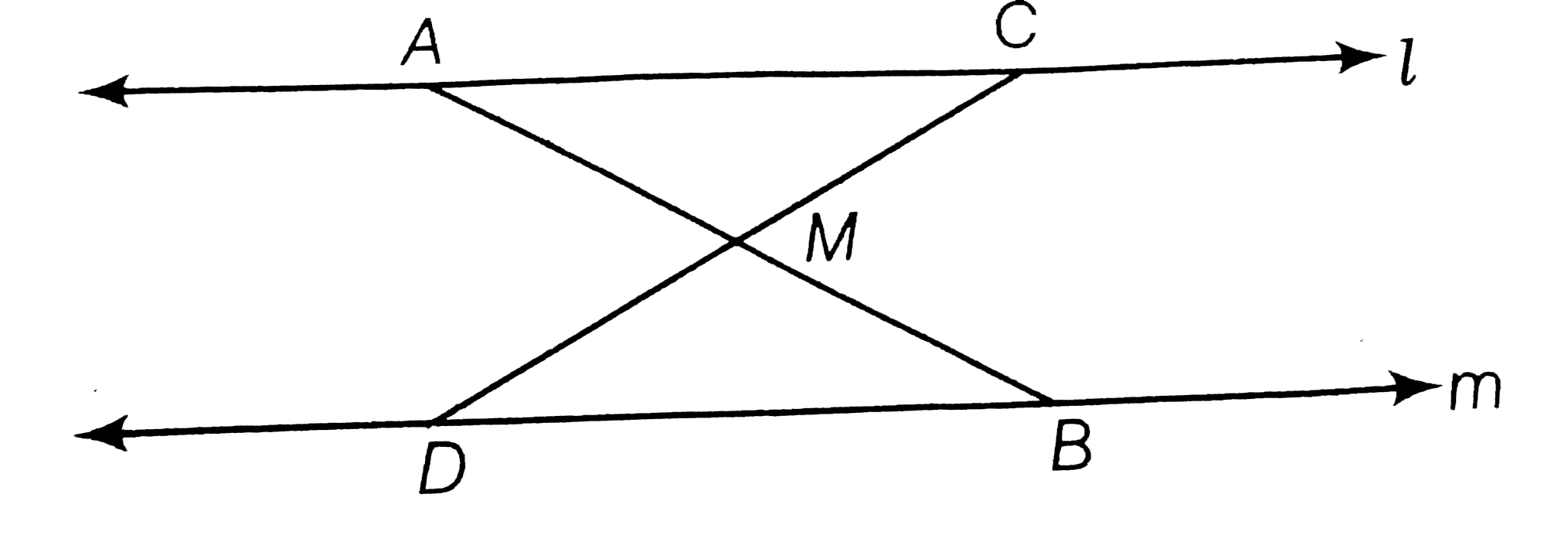
In Figure, $lIIm$
and M is the mid-point of the line segment $AB\stackrel{.}{}$
Prove that $M$
is also the mid-point of any line segment $CD$
having its end-points on $l$
and $m$
respectively.

Explanation

To prove that M is the midpoint of any line segment CD, where C is on line l and D is on line m, we will use the properties of congruent triangles. Here’s a step-by-step solution:

Step 1: Identify the Given Information
We know that:
- Lines l and m are parallel (l || m).
- M is the midpoint of line segment AB, which means AM = MB.

Step 2: Draw the Triangles
Consider triangles AMC and BMD, where:
- C is a point on line l.
- D is a point on line m.

Step 3: Establish Corresponding Angles
Since lines l and m are parallel:
- Angle 1 (∠AMC) is equal to Angle 3 (∠BMD) because they are alternate interior angles.
- Angle 2 (∠MAB) is equal to Angle 4 (∠MBD) because they are vertically opposite angles.

Step 4: Use the Given Lengths
Since M is the midpoint of AB, we have:
- AM = MB.

Step 5: Apply the Angle-Side-Angle (ASA) Congruence Criterion
Now we can state that:
- Triangle AMC is congruent to triangle BMD by the Angle-Side-Angle (ASA) congruence criterion, as we have:
- Angle 1 = Angle 3 (alternate angles)
- Angle 2 = Angle 4 (vertically opposite angles)
- AM = MB (given).

Step 6: Conclude that CM = DM
From the congruence of triangles AMC and BMD, we can conclude that:
- CM = DM.

Step 7: State that M is the Midpoint of CD
Since CM = DM, M is the midpoint of line segment CD.

Final Conclusion
Thus, we have proved that M is the midpoint of any line segment CD having its endpoints on lines l and m respectively.

---