Question

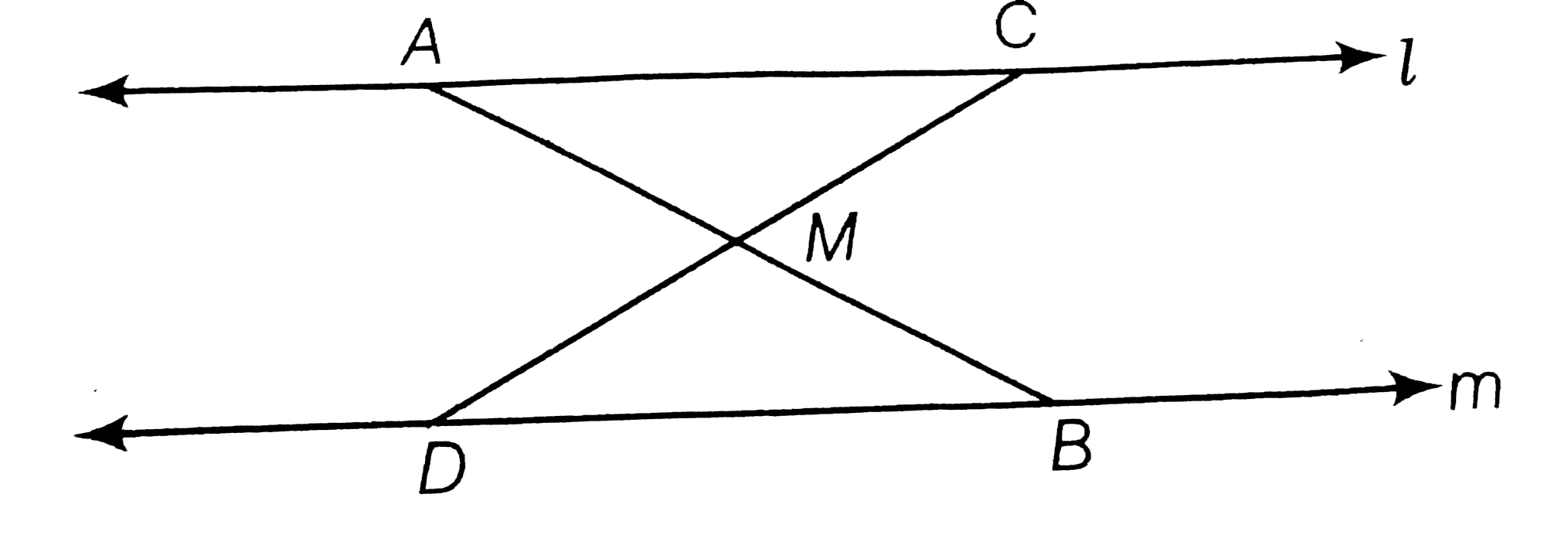
In Figure, $l\mid \mid m$
and $M$
is the mid-point of the
line segment $AB$
. Prove that $M$
is also the mid-pooint
of any line segment $CD$
having its end-points
on $landm$
respectively.

Explanation

To prove that point M is the midpoint of line segment CD, where points C and D lie on parallel lines l and m respectively, we will use the concept of congruent triangles.

1. Identify the Given Information:
- Lines l and m are parallel (l || m).
- M is the midpoint of line segment AB.
- Points C and D are on lines l and m respectively.

2. Draw the Triangles:
- We will consider triangles AMC and BMD.
- Here, A and B are the endpoints of the segment AB, and C and D are the endpoints of the segment CD.

3. Establish Corresponding Angles:
- Since l and m are parallel, the following angles are equal:
- Angle MAC = Angle MBD (vertically opposite angles).
- Angle A = Angle B (alternate interior angles).
- Angle C = Angle D (alternate interior angles).

4. List the Angles of the Triangles:
- In triangle AMC:
- Angle MAC
- Angle MCA
- Angle AMC
- In triangle BMD:
- Angle MBD
- Angle MDB
- Angle BMD

5. Use Angle-Angle-Angle (AAA) Criterion:
- We have established that:
- Angle MAC = Angle MBD
- Angle MCA = Angle MDB
- Angle AMC = Angle BMD
- Therefore, by the Angle-Angle-Angle (AAA) criterion, triangle AMC is congruent to triangle BMD.

6. Conclude from Congruent Triangles:
- Since triangles AMC and BMD are congruent, their corresponding sides are equal:
- AM = MB
- CM = MD

7. Final Conclusion:
- Since AM = MB and CM = MD, point M divides line segment CD into two equal parts.
- Therefore, M is the midpoint of line segment CD.

Hence, we have proved that M is the midpoint of CD.

---