Question

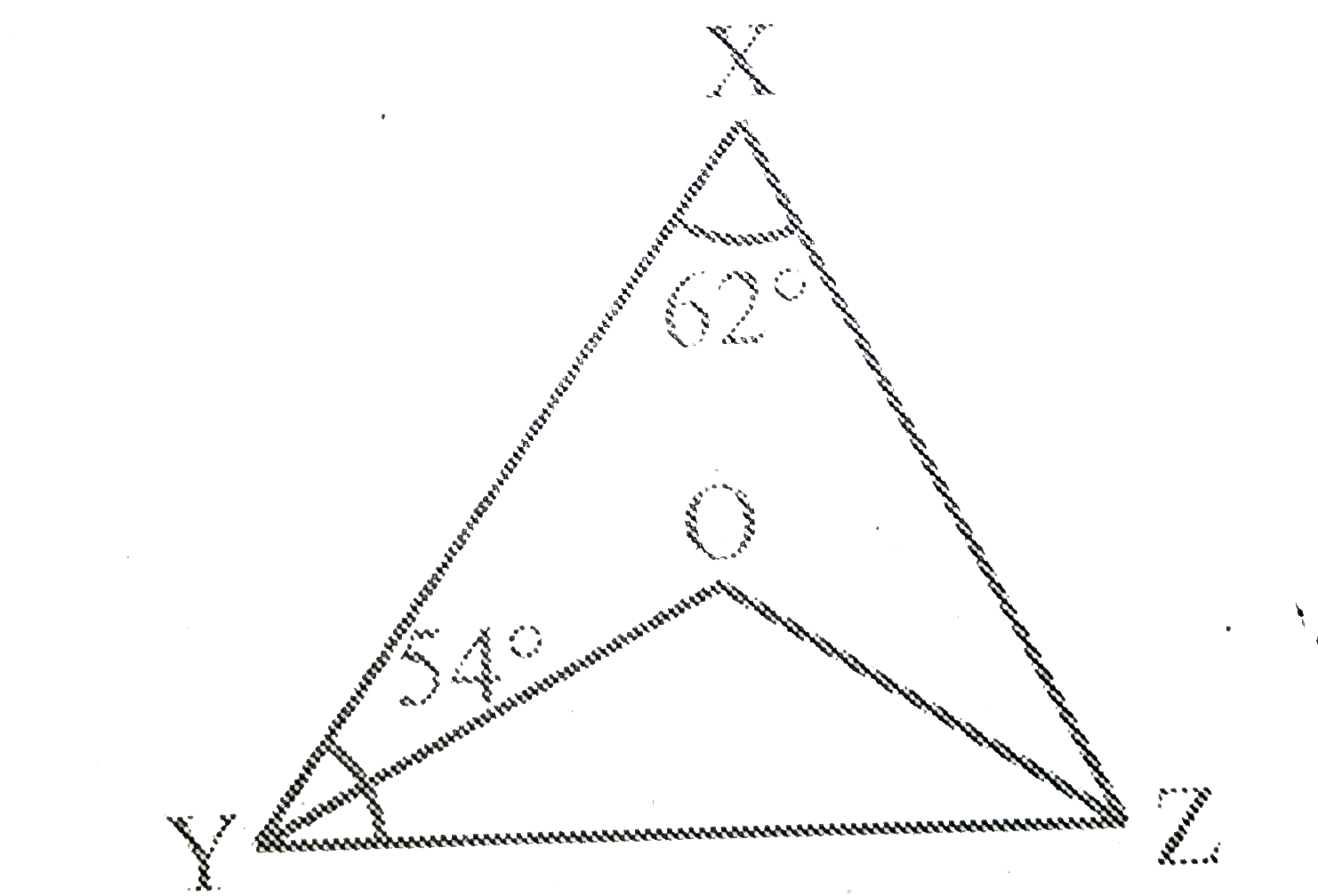
In Figure, $\angle X={62}^0,\angle XYZ={54}^0\stackrel{.}{}$
If $YO$
and $ZO$
are bisectors of $\angle XYZ$
and $\angle XZY$
respectively of $XYZ,$
find $\angle OZY$
and $\angle YOZ\stackrel{.}{}$

Figure

Explanation

To solve the problem, we will follow these steps:

Step 1: Identify the given angles
We have:
- Angle \( X = 62^\circ \)
- Angle \( XYZ = 54^\circ \)

Step 2: Use the angle sum property of a triangle
According to the angle sum property, the sum of the angles in triangle \( XYZ \) is \( 180^\circ \). Therefore, we can write:

\( \angle X + \angle XYZ + \angle XZY = 180^\circ \)

Substituting the known values:

\( 62^\circ + 54^\circ + \angle XZY = 180^\circ \)

Step 3: Calculate \( \angle XZY \)
Now, we can solve for \( \angle XZY \):

\( \angle XZY = 180^\circ - (62^\circ + 54^\circ) \)
\( \angle XZY = 180^\circ - 116^\circ = 64^\circ \)

Step 4: Find \( \angle OYZ \)
Since \( YO \) is the bisector of \( \angle XYZ \):

\( \angle OYZ = \frac{1}{2} \angle XYZ = \frac{1}{2} \times 54^\circ = 27^\circ \)

Step 5: Find \( \angle OZY \)
Since \( ZO \) is the bisector of \( \angle XZY \):

\( \angle OZY = \frac{1}{2} \angle XZY = \frac{1}{2} \times 64^\circ = 32^\circ \)

Step 6: Use the angle sum property in triangle \( YOZ \)
Now, in triangle \( YOZ \):

\( \angle YOZ + \angle OYZ + \angle OZY = 180^\circ \)

Substituting the known angles:

\( \angle YOZ + 27^\circ + 32^\circ = 180^\circ \)

Step 7: Calculate \( \angle YOZ \)
Now, we can solve for \( \angle YOZ \):

\( \angle YOZ = 180^\circ - (27^\circ + 32^\circ) \)
\( \angle YOZ = 180^\circ - 59^\circ = 121^\circ \)

Final Answers
- \( \angle OZY = 32^\circ \)
- \( \angle YOZ = 121^\circ \)

---