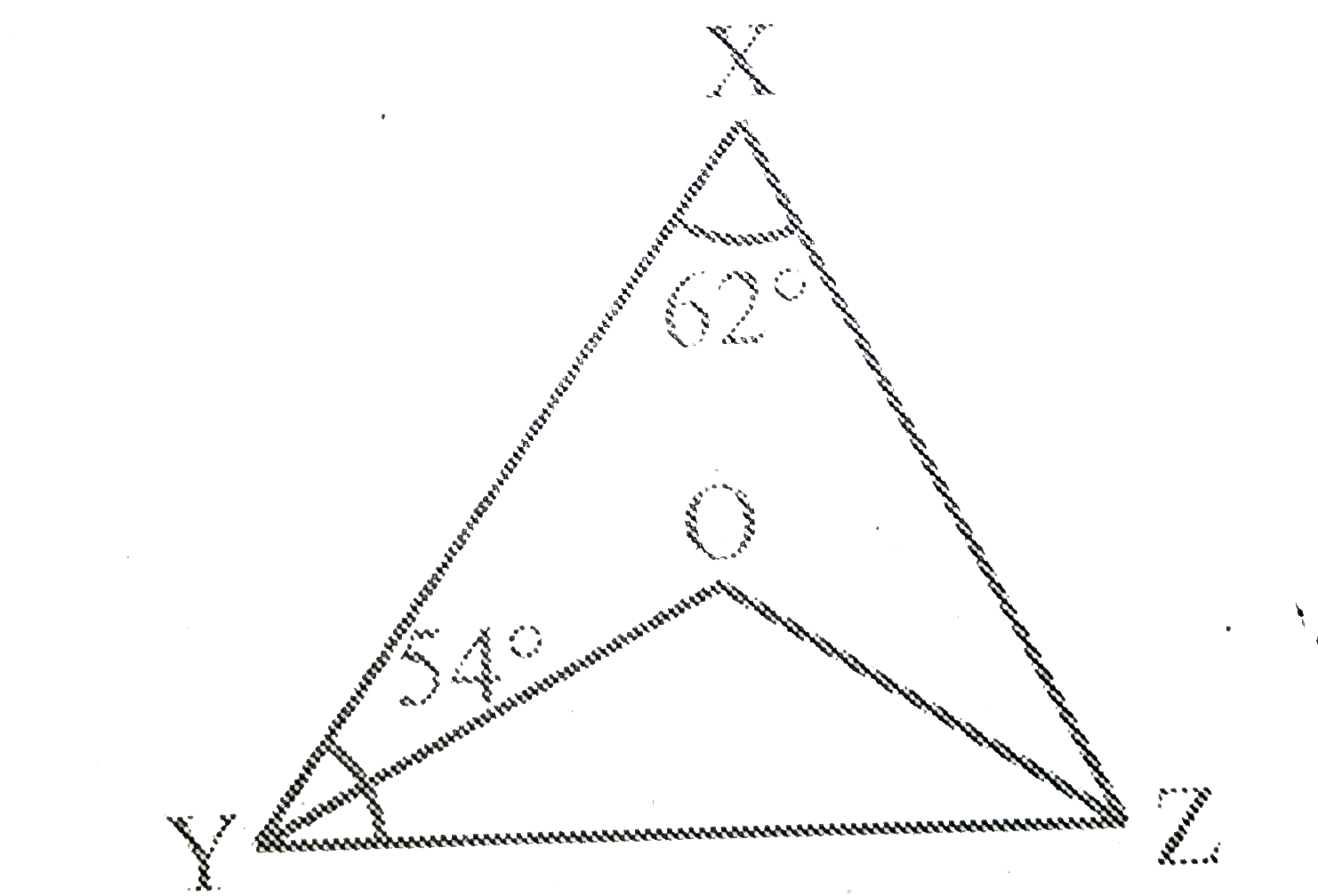
In Figure, ∠X=62∘, ∠XYZ=54∘. If YO and ZO are bisectors of ∠XYZ and ∠XZY respectively of XYZ, find ∠OZY and ∠YOZ.
To solve the problem step by step, we will use the properties of triangles and the fact that the sum of angles in a triangle is 180 degrees.
Step 1: Identify the given angles
We are given:
- Angle X=62∘
- Angle XYZ=54∘
Step 2: Find the third angle XZY
Using the property that the sum of angles in a triangle is 180 degrees, we can find angle XZY.
Sum of angles in triangle XYZ=180∘
X+XYZ+XZY=180∘
Substituting the known values:
62∘+54∘+XZY=180∘
116∘+XZY=180∘
XZY=180∘−116∘=64∘
Step 3: Find angle OZY
Since ZO is the bisector of angle XZY, we can find angle OZY by dividing angle XZY by 2.
OZY=XZY2=64∘2=32∘
Step 4: Find angle OYZ
Similarly, since YO is the bisector of angle XYZ, we can find angle OYZ by dividing angle XYZ by 2.
OYZ=XYZ2=54∘2=27∘
Step 5: Find angle YOZ
Now, we can find angle YOZ using the triangle property in triangle OYZ.
Sum of angles in triangle OYZ=180∘
OYZ+OZY+YOZ=180∘
Substituting the known values:
27∘+32∘+YOZ=180∘
59∘+YOZ=180∘
YOZ=180∘−59∘=121∘
Final Answers
- Angle OZY=32∘
- Angle YOZ=121∘
---
We are given:
- Angle X=62∘
- Angle XYZ=54∘
Using the property that the sum of angles in a triangle is 180 degrees, we can find angle XZY.
X+XYZ+XZY=180∘
Substituting the known values:
62∘+54∘+XZY=180∘
116∘+XZY=180∘
XZY=180∘−116∘=64∘
Since ZO is the bisector of angle XZY, we can find angle OZY by dividing angle XZY by 2.
Similarly, since YO is the bisector of angle XYZ, we can find angle OYZ by dividing angle XYZ by 2.
Now, we can find angle YOZ using the triangle property in triangle OYZ.
OYZ+OZY+YOZ=180∘
Substituting the known values:
27∘+32∘+YOZ=180∘
59∘+YOZ=180∘
YOZ=180∘−59∘=121∘
- Angle OZY=32∘
- Angle YOZ=121∘
Topper's Solved these Questions
Similar Questions
In Figure, ∠X=620,∠XYZ=540. If YO and ZO are bisectors of ∠XYZ and ∠XZY respectively of XYZ, find ∠OZY and ∠YOZ. Figure
View SolutionIn Fig. 6.40, ∠X=62∘,∠XYZ=54∘. If YO and ZO are the bisectors of ∠XYZ and ∠XZY respectively of ΔXYZ, find ∠OZY and ∠YOZ.
View SolutionIn Figure, O is the centre of the circle. If ∠CEA=300, find the values of x, y and z
View Solutionx is 5% of y, y is 24% of z . If x = 480 , find the values of y and z .
View SolutionIn Figure, find the value of x, y and z
View SolutionIf ax=b, by=c and cz=a, prove that xyz=1
View SolutionConstruct a triangle XYZ in which ∠Y=300, ∠Z=900 and XY+YZ+ZX=11cm
View SolutionIf [xy4z+6x+y]=[8w06] , then find the values of x, y, z and w .
View SolutionFrom the point P(a,b,c), let perpendicualars PLandPM be drawn to YOZandZOX planes, respectively. Then the equation of the plane OLM is a. xa+yb+zc=0 b. xa+yb−zc=0 c. xa−yb−zc=0 d. xa−yb+zc=0
View SolutionFrom the point P(a,b,c), let perpendicualars PLandPM be drawn to YOZandZOX planes, respectively. Then the equation of the plane OLM is a. xa+yb+zc=0 b. xa+yb−zc=0 c. xa−yb−zc=0 d. xa−yb+zc=0
View Solution