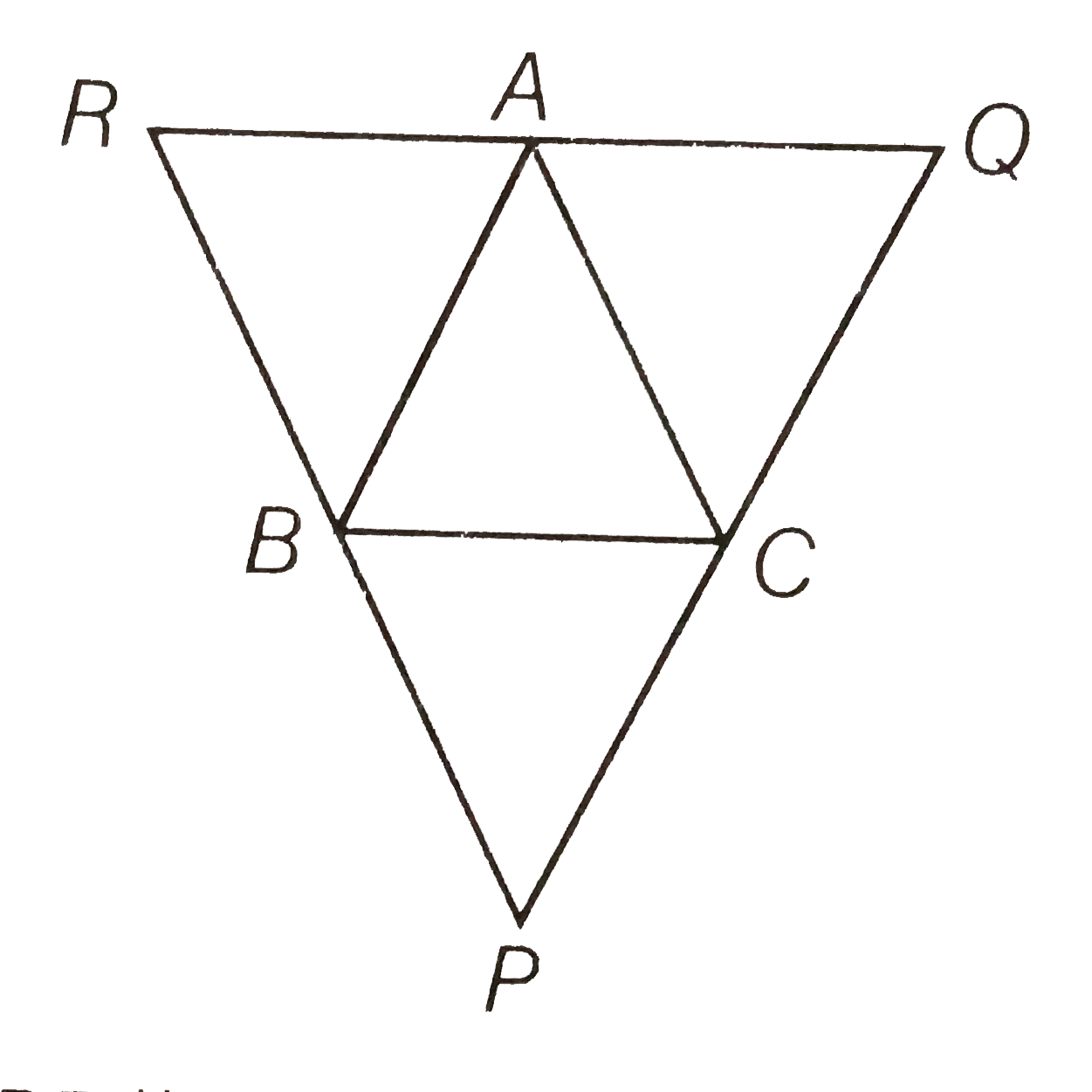
Given ABC , lines are drawn through A, B and C parallel respectively to the sides BC, CA and AB, forming triangle P Q R . Show that BC=1/2QR.
Step by step video & image solution for Given A B C , lines are drawn through A ,\ B\ a n d\ C parallel respectively to the sides B C ,\ C A\ a n d\ A B ,\ forming triangle P Q R . Show that BC=1/2QR. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Given △ABC , lines are drawn through A, B and C parallel respectively to the sides BC, CA and AB, forming △PQR.(Figure). Show that BC=12QR.
View SolutionThrough A, B and C lines RQ, PR and QP have been drawn, respectively parallel to sides BC, CA and AB of a ΔABC as shown in figure. Show that BC=12QR.
View SolutionIn Figure, two sides AB and BC and the median AD of ABC are equal respectively to the two sides PQ and QR and the median PM of the other triangle PQR. Prove that ABD≅PQM (ii) ABC ≅ PQR
View SolutionABC is a triangle and through A, B, C lines are drawn parallel to BC, CA and AB respectively intersecting at P, Q and R . Prove that the perimeter of PQR is double the perimeter of ABC
View SolutionIn the given figure, AD and CF are respectively perpendiculars to sides BC and AB of ABC. if ∠FCD=500, find ∠BAD.
View SolutionIn Figure, ABC is a right triangle right angled at A, BCED, ACFG and ABMN are squares on the sides BC, CA and AB respectively. Line segment AX ⊥DE meets BC at Y. Show that: ar (BYXD)=ar (ABMN).
View SolutionIn Figure, ABC is a right triangle right angled at A, BCED, ACFG and AMN are square on the sides BC, CA and AB respectively. Line segment AX ⊥DE meets BC at Y. Show that: ar (BYXD)=2 ar ( MBC)
View SolutionIn Figure, ABC is a right triangle right angled at A, BCED, ACFG and ABMN are square on the sides BC, CA and AB respectively. Line segment AX ⊥DE meets BC at Y. Show that: ar(CYXE)=ar (ACFG)
View SolutionIn Figure, ABC is a right triangle right angled at A, BCED, ACFG and AMN are square on the sides BC, CA and AB respectively. Line segment AX ⊥DE meets BC at Y. Show that: MBC ≅ ABD
View SolutionIn a ABC,D and E are points on sides ABandAC respectively such that BD=CE. If ∠B=∠C, show that DE∣∣BC.
View Solution
