Question

$BM$
and $CN$
are perpendiculars to a line passing through the vertex $A$
of a triangle $ABC\stackrel{.}{}$
If $L$
is the mid-point of $BC,$
prove that $LM=LN\stackrel{.}{}$

Explanation

To prove that $$LM=LN$$ in triangle $$ABC$$ with the given conditions, we will follow these steps:

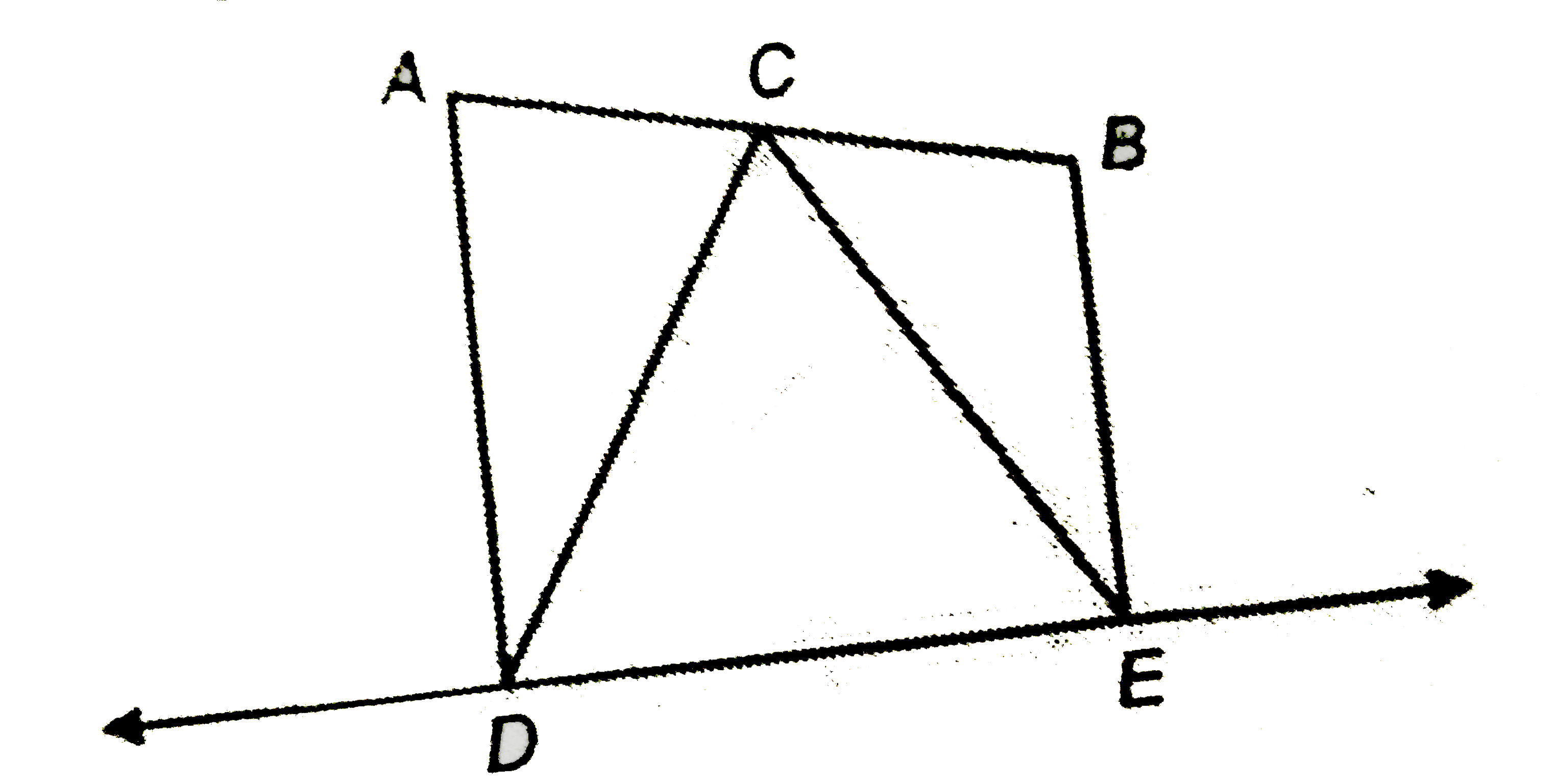
Step 1: Understand the Setup
We have triangle \( ABC \) with points \( B \) and \( C \) on a line, and points \( M \) and \( N \) are perpendiculars dropped from points \( B \) and \( C \) to a line passing through vertex \( A \). Point \( L \) is the midpoint of segment \( BC \).

Hint: Visualize the triangle and the perpendiculars to understand the relationships between the points.

Step 2: Establish Relationships
Since \( L \) is the midpoint of \( BC \), we have:
\( BL = LC \)
This means that the lengths from \( B \) to \( L \) and from \( L \) to \( C \) are equal.

Hint: Remember that the midpoint divides the segment into two equal parts.

Step 3: Draw Perpendiculars
Draw a line \( OL \) that is perpendicular to \( MN \). Since \( BM \) and \( CN \) are both perpendicular to the line through \( A \), we can conclude that:
\( BM \parallel CN \)
This implies that the angles formed with line \( OL \) are equal.

Hint: Use the properties of parallel lines and transversals to identify equal angles.

Step 4: Identify Equal Intercepts
Since \( BC \) is a transversal line to the three parallel lines \( BM \), \( CN \), and \( OL \), by the property of equal intercepts, we have:
\( OM = ON \)
This means that the segments \( OM \) and \( ON \) are equal.

Hint: Recall that equal intercepts on parallel lines imply equal lengths.

Step 5: Analyze Triangles
Now, consider triangles \( OLM \) and \( OLN \):
- We have \( OM = ON \) (from the previous step).
- The line \( OL \) is common to both triangles.
- The angles \( \angle LOM \) and \( \angle LON \) are both \( 90^\circ \).

Hint: Use the properties of congruent triangles to establish equality.

Step 6: Apply the SAS Congruence Criterion
By the SAS (Side-Angle-Side) congruence criterion:
\( \triangle OLM \cong \triangle OLN \)
This implies that:
\( LM = LN \)

Hint: Remember that corresponding parts of congruent triangles are equal.

Conclusion
Thus, we have proved that:
\( LM = LN \)

This completes the proof that the lengths from the midpoint \( L \) to points \( M \) and \( N \) are equal.