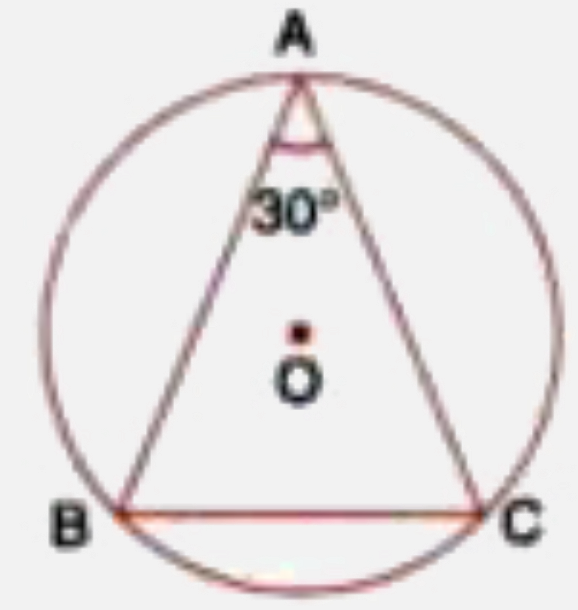
In Figure, ABC is a triangle in which ∠BAC=30∘. Show that BC is the radius of the circumcircle of ABC, whose centre is O.
Step by step video & image solution for In Figure, A B C is a triangle in which /_B A C=30^@. Show that B C is the radius of the circumcircle of A B C , whose centre is O. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
In the given figure , ABC is a triangle in which ∠BAC=30∘ . Show that BC is equal to the radius of the circumcircle of the traiangle ABC , whose centre is O.
View SolutionIn Figure, ABC is an equilateral triangle. Find m ∠BEC
View SolutionIn Figure, O is the centre of the circle. Find ∠BAC
View SolutionIn Figure, if ABC is an equilateral triangle. Find ∠BDC and ∠BEC
View SolutionIn Figure, ABC is an isosceles triangle in which AB=AC.andCP∣∣AB and AP is the bisector of exterior ∠CAD of ABC . Prove that ∠PAC=∠BCA and (ii) ABCP is a parallelogram.
View SolutionIn triangle ABC,a:b:c=4:5:6. The ratio of the radius of the circumcircle to that of the incircle is____.
View SolutionIn triangle ABC,a:b:c=4:5:6. The ratio of the radius of the circumcircle to that of the incircle is____.
View SolutionIn figure, ABC is a triangle in which ∠ABC=90∘and AD⊥BC. Prove that AC2=AB2+BC2−2BC.BD.

View SolutionIn figure, ABCD is a trapezium in which AB∣∣CD . Prove that: ar(△AOD)=ar(△BOC).
View SolutionABC is a triangle in which ∠A=90o, AN⊥BC, BC=12cm and AC=5cm . Find the ratio of the areas of ANC and ABC.
View Solution
