Question

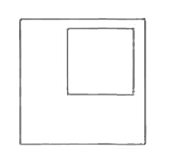
In the Figure, a square dart board is shown. The length of a side of
the larger square is 1.5 times the length of a side of the smaller square. If
a dart is thrown and lands on the larger square. What is the probability that
it will land in the interior of the smaller square?

Explanation

To solve the problem, we will follow these steps:

Step 1: Define the side lengths of the squares
Let the length of a side of the smaller square be \( a \). According to the problem, the length of a side of the larger square is 1.5 times the length of the smaller square. Therefore, the side length of the larger square is:
\( 1.5a \)

Step 2: Calculate the area of the smaller square
The area of a square is given by the formula:
\( \text{Area} = \text{side}^2 \)
Thus, the area of the smaller square is:
\( \text{Area of smaller square} = a^2 \)

Step 3: Calculate the area of the larger square
Using the same formula for the area, the area of the larger square is:
\( \text{Area of larger square} = (1.5a)^2 = 2.25a^2 \)

Step 4: Set up the probability formula
The probability \( P \) that the dart will land in the interior of the smaller square when thrown at the larger square is given by the ratio of the area of the smaller square to the area of the larger square:
\( P = \frac{\text{Area of smaller square}}{\text{Area of larger square}} = \frac{a^2}{2.25a^2} \)

Step 5: Simplify the probability expression
We can simplify the expression:
\( P = \frac{a^2}{2.25a^2} = \frac{1}{2.25} \)
Now, converting \( 2.25 \) into a fraction:
\( 2.25 = \frac{9}{4} \)
Thus:
\( P = \frac{1}{\frac{9}{4}} = \frac{4}{9} \)

Final Answer
The probability that the dart will land in the interior of the smaller square is:
\( \boxed{\frac{4}{9}} \)