A target shown in Figure, consists of three concentric circles of radii 3,7 and 9cm respectively. A dart is thrown and lands on the target. What is probability that the dart will and on the shaded region?
To solve the problem, we need to find the probability that a dart thrown at a target consisting of three concentric circles lands in the shaded region. The circles have radii of 3 cm, 7 cm, and 9 cm respectively.
1. Identify the Areas of the Circles:
- The area of a circle is given by the formula A=πr2.
- For the innermost circle (radius 3 cm):
A1=π(32)=π×9=9π cm2
- For the second circle (radius 7 cm):
A2=π(72)=π×49=49π cm2
- For the outermost circle (radius 9 cm):
A3=π(92)=π×81=81π cm2
2. Calculate the Area of the Shaded Region:
- The shaded region is the area between the second circle (radius 7 cm) and the outermost circle (radius 9 cm).
- To find the area of the shaded region, subtract the area of the second circle from the area of the outermost circle:
Area of shaded region=A3−A2=81π−49π=32π cm2
3. Calculate the Total Area of the Target:
- The total area of the target is the area of the outermost circle:
Total area=A3=81π cm2
4. Calculate the Probability:
- The probability P that the dart lands in the shaded region is given by the ratio of the area of the shaded region to the total area of the target:
P=Area of shaded regionTotal area=32π81π
- The π cancels out:
P=3281
Final Answer:
The probability that the dart will land in the shaded region is 3281.
- The area of a circle is given by the formula A=πr2.
- For the innermost circle (radius 3 cm):
A1=π(32)=π×9=9π cm2
- For the second circle (radius 7 cm):
A2=π(72)=π×49=49π cm2
- For the outermost circle (radius 9 cm):
A3=π(92)=π×81=81π cm2
- The shaded region is the area between the second circle (radius 7 cm) and the outermost circle (radius 9 cm).
- To find the area of the shaded region, subtract the area of the second circle from the area of the outermost circle:
Area of shaded region=A3−A2=81π−49π=32π cm2
- The total area of the target is the area of the outermost circle:
Total area=A3=81π cm2
- The probability P that the dart lands in the shaded region is given by the ratio of the area of the shaded region to the total area of the target:
P=Area of shaded regionTotal area=32π81π
- The π cancels out:
P=3281
The probability that the dart will land in the shaded region is 3281.
Topper's Solved these Questions
Similar Questions
In figure, a dart is thrown and lands in the interior of the circle. What is the probability that the dart will land in the shaded region?
View SolutionIn the Figure, a square dart board is shown. The length of a side of the larger square is 1.5 times the length of a side of the smaller square. If a dart is thrown and lands on the larger square. What is the probability that it will land in the interior of the smaller square?
View SolutionIn Figure, there are shown sectors of two concentric circles of radii 7cm and 3.5cm. Find the area of the shaded region.
(π=227)
View SolutionIn Figure, there are shown sectors of two concentric circles of radii 7cm and 3.5cm. Find the area of the shaded region. (Useπ227)
View SolutionFind the area of the shaded region in Figure, where radii of the two concentric circles with centre O are 7 cm and 14 cm respectively and ∠AOC=40∘ .
View SolutionSuppose you drop a die at random on the rectangular region shown in Figure. What is the probability that it will land inside the circle with diameter 1m?
View SolutionThe boundary of the shaded region in the given figure consists of three semicircular areas, the smaller ones being equal. If the diameter of the larger one is 14 cm, calculate
(i) the length of the boundary
(ii) the area of the shaded region
View Solution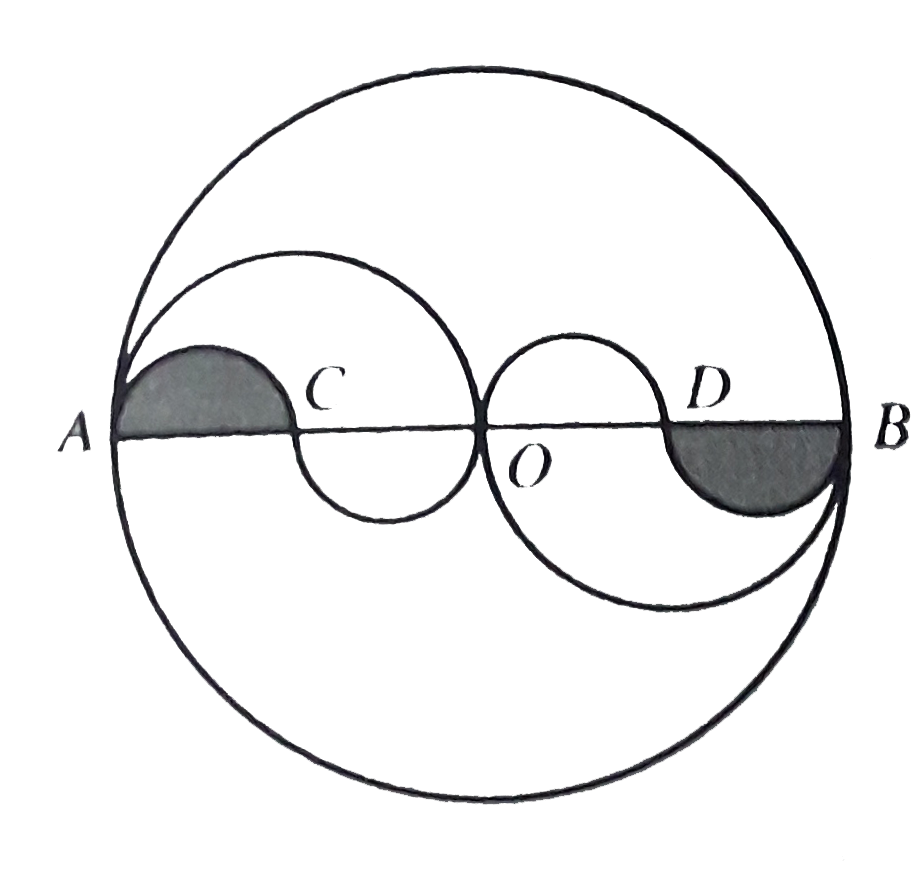
In the circle shown above, O is the center and ¯¯¯¯¯¯AB is a diameter . There are two semicircles with diameters ¯¯¯¯¯¯AO and ¯¯¯¯¯¯BO , and four smaller semicircles with congruent diameters ¯¯¯¯¯¯AC,¯¯¯¯¯¯CO,¯¯¯¯¯¯OD and ¯¯¯¯¯¯DB . A point is picked at random in the large circle . What is the probability that it lands in a shaded region ?
View SolutionIn the given figure, A, B, C and D are centres of four circles that have a radius of 1 unit. If a point is selected at random from interior of square ABCD, then what is the probability that it lies in the shaded region
View SolutionTwo aeroplanes I and II bomb a target in succession. The probabilities of I and II scoring a hit correctly are 0.3 and 0.2, respectively. The second plane will bomb only if the first misses the target. The probability that the target is hit by the second plane is (A) 0.06 (B) 0.14 (C) 722 (D) 0.7
View Solution
