A circular field has a circumference of 360km. Three cyclists start together and can cycle 48, 60 and 72 km, a day, round the field. When will they meet again?
To solve the problem of when the three cyclists will meet again after starting together, we need to follow these steps:
1. Determine the time taken by each cyclist to complete one round of the circular field:
- Cyclist 1 can cycle 48 km in a day. To find out how many days it takes to complete one round (360 km):
Time for Cyclist 1=360 km48 km/day=7.5 days
- Cyclist 2 can cycle 60 km in a day. To find out how many days it takes to complete one round:
Time for Cyclist 2=360 km60 km/day=6 days
- Cyclist 3 can cycle 72 km in a day. To find out how many days it takes to complete one round:
Time for Cyclist 3=360 km72 km/day=5 days
2. Convert the time taken by each cyclist into hours:
- For Cyclist 1:
7.5 days=7.5×24=180 hours
- For Cyclist 2:
6 days=6×24=144 hours
- For Cyclist 3:
5 days=5×24=120 hours
3. Find the least common multiple (LCM) of the times in hours:
- We need to find the LCM of 180, 144, and 120.
- The prime factorization of each number is:
- 180=22×32×5
- 144=24×32
- 120=23×3×5
- The LCM is found by taking the highest power of each prime:
LCM=24×32×5=720 hours
4. Convert the LCM back into days:
- Now, we convert 720 hours into days:
Days=720 hours24 hours/day=30 days
5. Conclusion:
- The three cyclists will meet again after 30 days.
- Cyclist 1 can cycle 48 km in a day. To find out how many days it takes to complete one round (360 km):
Time for Cyclist 1=360 km48 km/day=7.5 days
Time for Cyclist 2=360 km60 km/day=6 days
Time for Cyclist 3=360 km72 km/day=5 days
- For Cyclist 1:
7.5 days=7.5×24=180 hours
6 days=6×24=144 hours
5 days=5×24=120 hours
- We need to find the LCM of 180, 144, and 120.
- The prime factorization of each number is:
- 180=22×32×5
- 144=24×32
- 120=23×3×5
LCM=24×32×5=720 hours
- Now, we convert 720 hours into days:
Days=720 hours24 hours/day=30 days
- The three cyclists will meet again after 30 days.
Topper's Solved these Questions
Similar Questions
There is a circular path around a sports field. Soma takes 18 minutes to drive one round of the field, while Ravi takes 12 minutes for the same. Suppose they both start at the same point and at the same time, and go in the same direction. After how many minutes will they meet again at the starting point?
View SolutionThere is a circular path around a sports field. Priya takes 18 minutes to drive on round of the field, while Ravish takes 12 minutes for the same. Suppose they both start at the same point and at the same time, and go in the same direction. After how many minutes will they meet again at the starting point?
View SolutionA circular coil has moment of inertia 0.8 kg m2 around any diameter and is carrying current to produce a magnetic moment of 20Am2. The coil is kept initially in a vertical position and it can rotate freely around a horizontal diameter. When a uniform magnetic field of 4 T is applied along the vertical, it starts rotating around its horizontal diameter. The angular speed the coil acquires after rotating by 60∘ will be :
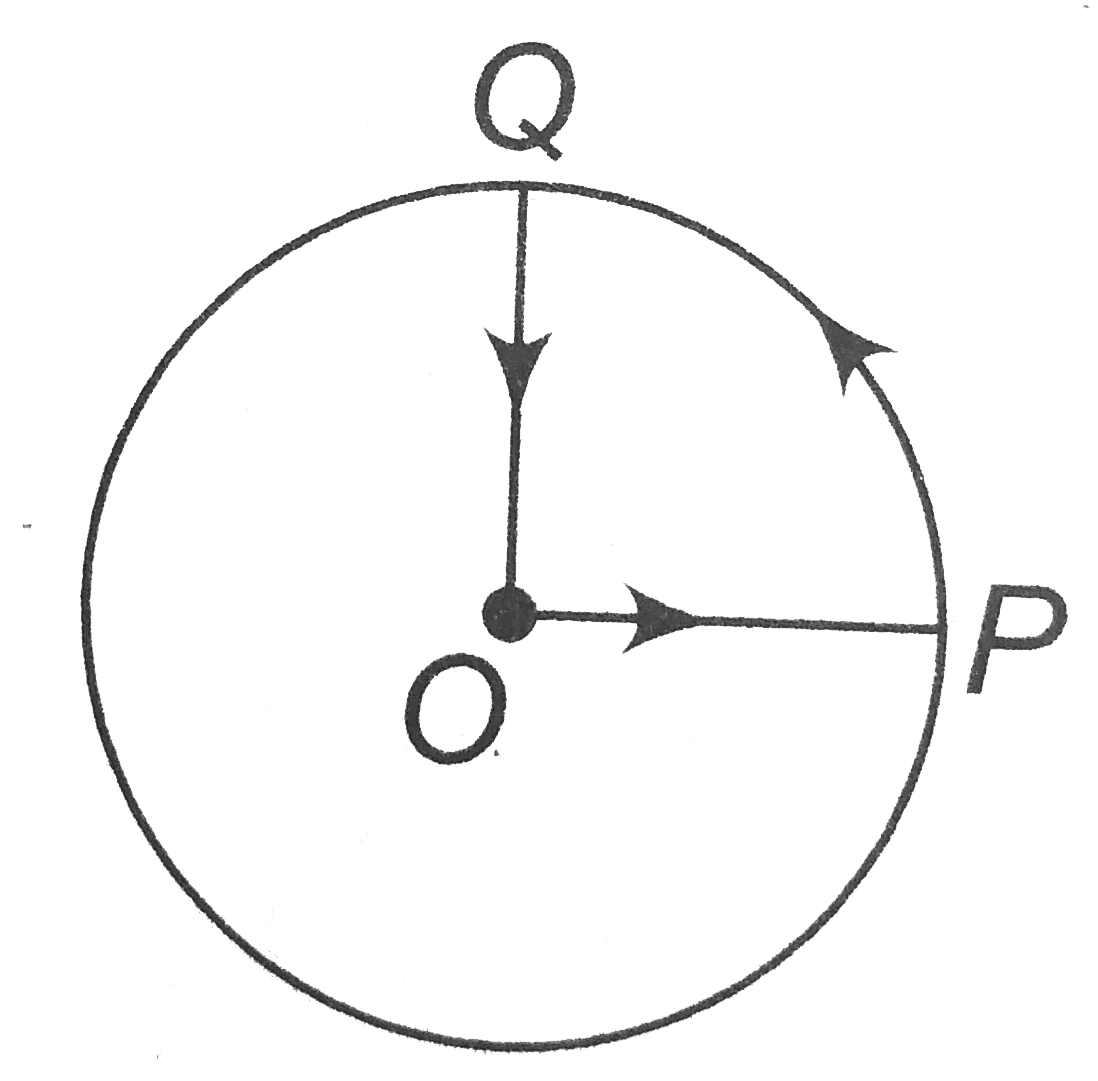
View SolutionA cyclist starts from the center O of a circular park of radius 1km, reaches the edge P of the park, then cycles along the PQ circumference and returns to the center along OQ as shown in fig. If the round trip taken ten minute, the (a) net displacement, (b) average velocity and (c) average speed of the cyclists (in kilometer per hour) is
View SolutionA 10−km long straight road connects two towns A and B, Two cyclists dimultaneously start one from town A and the other from town B .On reaching the opposite town, a cyclists simmediaeately retrns to his starting town wheras the other cyclist takes some rest and then returns to his starting town. Both of them can ride at speed 20kmh−1 in absence of wind but during their whole journey uniform wind from town A and B increase the speed of it decreases the speed of the cyclist going against the wind Both the cyclisrs meet twice, first at 2 km and then 6 km away from one of the tomns. If which town and for what perild does a cyclist rest ?
View SolutionA cyclist starts from the centre O of a circular park of radius 1km, reaches the edge P of the park, then cycles along the PQ cicumference and returns to the centre along OQ as shown in fig. If the round trip taken ten minute, the net displacement and average speed of the cylists (in kilometer and kinetic per hour) is

View SolutionThe area of a square field is 60025 m2. A man cycles along its boundary at 18 km/ hr. In how must time will he return at the starting point ?
View SolutionA driver having a definite reaction time is capable of stopping his car over a distance of 30 m on seeing a red traffic signal, when the speed of the car is 72 km/hr andover a distance of 10 m when the speed is 36 km/hr. Find the distance over which he can stop the car if it were running at a speed of 54 km/hr. Assume that his reaction time and the deceleration of the car remains same in all the three cases.
View SolutionA circular coil of radius 2.00 cm has 50 turns. A uniform magnetic field B= 0.200 T exists in the space is a direction parallel to the axis of the loop. The coil is now rotated about a diameter through an angle of 60.0∘. The operation takes 0.100 s. (a) find the average emf induced in the coil. (b) if the coil is a closed one(with the two ends joined together) and has a resistance of 4.00Ω. calculate the net charge crossing a cross- section of the wire of the coil.
View SolutionA dence collection of equal number of electrona and positive ions is called netural plasma. Certain solids contianing fixed positive ions surroundedby free electrons can be treated as neytral plasma. Let 'N' be the numbrer density of free electrons, each of mass 'm'. When the elctrons are subjected to an eletric field, they are displaced relatively away from the heavy positive ions. if the electric field becomes zero, the electrons begin to oscillate about the positive ions with a natural angular frequency 'ωP' which is called the plasma frequency. to sustain the oscillations, a time varying electric field needs to be applied that has an angular frequrncy ω, where a part of the energy is absorbed and a part of it is reflected. As ω approaches ωp all the free electrons are set to resonance together and all the energy is reflected. this is the explaination of high reflectivity of metals.
(2) Estimate the wavelength at which plasma reflection will occur for a metal having the density of electrons N≈4×1027m−3. Taking ε0=1011 and mass m≈10−30, where these quantities are in proper SI units.
View Solution
