A tower stands near an airport. The angle of elevation θ of the tower from a point on the ground such that its tangent is 512. Find the height of the tower, if the distance of the observer from the tower is 120m.
To find the height of the tower based on the given information, we can follow these steps:
Step 1: Understand the problem
We have a tower and an observer at a distance of 120 meters from the base of the tower. The angle of elevation from the observer to the top of the tower has a tangent value of 512.
Step 2: Set up the triangle
Let:
- AB be the height of the tower (which we need to find).
- BC be the distance from the observer to the tower, which is given as 120 meters.
- θ be the angle of elevation from the observer to the top of the tower.
Step 3: Use the tangent function
From the definition of tangent in a right triangle, we know:
tan(θ)=oppositeadjacent=ABBC
Substituting the known values:
tan(θ)=h120
where h is the height of the tower.
Step 4: Set up the equation
We know from the problem that:
tan(θ)=512
So we can set up the equation:
h120=512
Step 5: Cross-multiply to solve for h
Cross-multiplying gives us:
h⋅12=5⋅120
This simplifies to:
12h=600
Step 6: Solve for h
Now, divide both sides by 12:
h=60012=50
Conclusion
The height of the tower h is 50 meters.
We have a tower and an observer at a distance of 120 meters from the base of the tower. The angle of elevation from the observer to the top of the tower has a tangent value of 512.
Let:
- AB be the height of the tower (which we need to find).
- BC be the distance from the observer to the tower, which is given as 120 meters.
- θ be the angle of elevation from the observer to the top of the tower.
From the definition of tangent in a right triangle, we know:
tan(θ)=oppositeadjacent=ABBC
Substituting the known values:
tan(θ)=h120
where h is the height of the tower.
We know from the problem that:
tan(θ)=512
So we can set up the equation:
h120=512
Cross-multiplying gives us:
h⋅12=5⋅120
This simplifies to:
12h=600
Now, divide both sides by 12:
h=60012=50
The height of the tower h is 50 meters.
Topper's Solved these Questions
Similar Questions
In figure, the angle of elevation of the top of a tower AC from a point B on the ground is 60∘. If the height of the tower is 20m , find the distance of the point from the foot of the tower.
View SolutionIn figure, the angle of elevation of the top of a tower AC from a point B on the ground is 60∘. If the height of the tower is 20m , find the distance of the point from the foot of the tower.
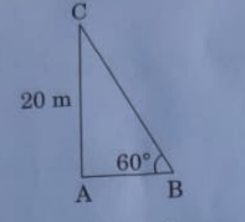
View SolutionIn figure , the angle of elevation of the top of a tower AC from a point B on the ground is 60∘ . If the height of the tower is 20 m, Find the distance of the point from the foot of the power .

View SolutionThe angle of elevation of the top of a tower from a point on the ground, which is 30m away from the foot of the tower is 30∘ . Find the height of the tower.
View SolutionThe angle of elevation of the top of a tower from a point on the ground, which is 30m away from the foot of the tower, is 30∘. Find the height of the tower.
View SolutionThe angle of elevation of the top of a tower from a point on the ground, which is 30 m away from the foot of the tower is 30∘. Find the height of the tower.
View SolutionThe angle of elevation of the top of a tower from a point on the ground is 60∘. which is 25 m away from the foot of the tower. Find the height of the tower
View SolutionThe angle of elevation of the top of a tower from a point 40 m away from its foot is 60∘. Find the height of the tower.
View SolutionIn the figure-2, the angle of elevation of the top of tower AC from a point B on the ground is 60∘ . If the height of the tower is 20 m. find the distance of the point from the foot of the tower.

View SolutionThe angle of elevation of the top of a tower at a point on the ground is 30∘ . What will be the angle of elevation, if the height of the tower is tripled?
View Solution
