A toy is in the shape of a right circular cylinder with a hemisphere on one end and a cone on the other. The height and radius of the cylindrical par are 13cm and 5cm respectively. The radii of the hemispherical and conical parts re the same as that of the cylindrical part. Calculate the surface area of the toy if height of the conical part is 12 cm.
To solve the problem step by step, we will calculate the surface area of the toy, which consists of a right circular cylinder, a hemisphere, and a cone.
Step 1: Identify the dimensions
- Height of the cylindrical part (h_cylinder) = 13 cm
- Radius of the cylinder, hemisphere, and cone (r) = 5 cm
- Height of the conical part (h_cone) = 12 cm
Step 2: Calculate the surface area of the hemisphere
The formula for the curved surface area of a hemisphere is:
Surface Area of Hemisphere=2πr2
Substituting the values:
Surface Area of Hemisphere=2π(5)2=2π(25)=50πcm2
Step 3: Calculate the surface area of the cylinder
The formula for the curved surface area of a cylinder is:
Surface Area of Cylinder=2πrh
Substituting the values:
Surface Area of Cylinder=2π(5)(13)=130πcm2
Step 4: Calculate the slant height of the cone
The slant height (l) of the cone can be calculated using the Pythagorean theorem:
l=√r2+h2cone
Substituting the values:
l=√(5)2+(12)2=√25+144=√169=13cm
Step 5: Calculate the surface area of the cone
The formula for the curved surface area of a cone is:
Surface Area of Cone=πrl
Substituting the values:
Surface Area of Cone=π(5)(13)=65πcm2
Step 6: Calculate the total surface area of the toy
The total surface area (A) of the toy is the sum of the surface areas of the hemisphere, cylinder, and cone:
A=Surface Area of Hemisphere+Surface Area of Cylinder+Surface Area of Cone
Substituting the values:
A=50π+130π+65π=245πcm2
Step 7: Calculate the numerical value
Using π≈3.14:
A≈245×3.14≈769.3cm2
Final Answer
The surface area of the toy is approximately 769.3cm2.
- Height of the cylindrical part (h_cylinder) = 13 cm
- Radius of the cylinder, hemisphere, and cone (r) = 5 cm
- Height of the conical part (h_cone) = 12 cm
The formula for the curved surface area of a hemisphere is:
Surface Area of Hemisphere=2πr2
Substituting the values:
Surface Area of Hemisphere=2π(5)2=2π(25)=50πcm2
The formula for the curved surface area of a cylinder is:
Surface Area of Cylinder=2πrh
Substituting the values:
Surface Area of Cylinder=2π(5)(13)=130πcm2
The slant height (l) of the cone can be calculated using the Pythagorean theorem:
l=√r2+h2cone
Substituting the values:
l=√(5)2+(12)2=√25+144=√169=13cm
The formula for the curved surface area of a cone is:
Surface Area of Cone=πrl
Substituting the values:
Surface Area of Cone=π(5)(13)=65πcm2
The total surface area (A) of the toy is the sum of the surface areas of the hemisphere, cylinder, and cone:
A=Surface Area of Hemisphere+Surface Area of Cylinder+Surface Area of Cone
Substituting the values:
A=50π+130π+65π=245πcm2
Using π≈3.14:
A≈245×3.14≈769.3cm2
The surface area of the toy is approximately 769.3cm2.
Topper's Solved these Questions
Similar Questions
A toy is in the shape of a right circular cylinder with a hemisphere on one end and a cone on the other. The height and radius of the cylindrical part are 13cm and 5cm respectively. The radii of the hemispherical and conical parts are the same as that of the cylindrical part. Calculate the surface area of the toy if height of the conical part is 12 cm.
View SolutionA toy is in the shape of a right circular cylinder with a hemisphere on one end and a cone on the other. The height and radius of the cylindrical part are 13cm and 5cm respectively. The radii of the hemispherical and conical parts are the same as that of the cylindrical part. Calculate the surface area of the toy if height of the conical part is 12cm.
View SolutionA toy is in the shape of a right circular cylinder with a hemisphere on one end and a cone on the other. The height and radius of the cylindrical part are 13cm and 5cm respectively. The radii of the hemispherical and conical parts are the same as that of the cylindrical part. Calculate the surface area of the toy if height of the conical part is 12cm.
View SolutionA solid is in the form of a right circular cylinder, with a hemisphere at one end and a cone at the other end. The radius of the common base is 3.5 cm and the heights of the cylindrical and conical portions are 10 cm and 6 cm, respectively. Find the total surface area of the solid. (Use π=22/7 )
View SolutionA solid toy is in the form of a right circular cylinder with a hemispherical shape at one end and a cone at the other end. Their common diameter is 4.2 cm. and the height of the cylindrical and conical portions are 12 cm and 7 cm respectively. Find the volume of the solid toy. (Use π=22/7 )
View SolutionFind the total surface area of a right circular cone with radius 6cm and height 8cm.
View SolutionA rocket is in the form of a right circular cylinder closed at the lower end and surmounted by a cone with the same radius as that of the cylinder. The diamter and height of the cylinder are 6 cm and 12 cm , respectively. If the slant height of the conical portion is 5 cm, the find the total surface area and volume of the rocket. ( use π=3.14).
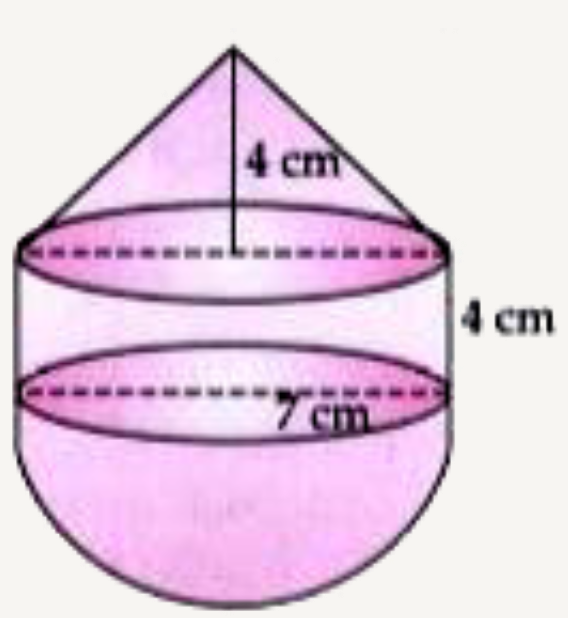
View SolutionThe following figure represents a solid consiting of right circular cylinder with a hemisphere at one end and a cone at the other. Their common radius is 7 cm. The height of the cylinder and cone are each of 4 cm. Find the volume of the solid.
View SolutionA solid wooden toy is in the shape of a right circular cone mounted on a hemisphere. If the radius of the hemisphere is 4.2 cm and the total height of the toy is 10.2 cm, find the volume of the wooden toy.
View SolutionA solid wooden toy is in the shape of a right circular cone mounted on a hemisphere. If the radius of the hemisphere is 4.2 cm and the total height of the toy is 10.2 cm, find the volume of the wooden toy.
View Solution
