Question

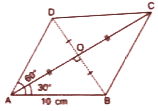
A rhombus of side 20cm has two angles of ${60}^0$
each. Find the length of the diagonals.

Explanation

To find the lengths of the diagonals of a rhombus with a side length of 20 cm and two angles of 60 degrees each, we can follow these steps:

Step 1: Understand the properties of the rhombus
A rhombus has the following properties:
- All sides are equal.
- The diagonals bisect each other at right angles (90 degrees).
- The diagonals also bisect the angles of the rhombus.

Step 2: Label the rhombus
Let's label the rhombus as ABCD, where:
- AB = BC = CD = DA = 20 cm (sides of the rhombus)
- ∠A = ∠C = 60 degrees
- ∠B = ∠D = 120 degrees (since the sum of angles in a quadrilateral is 360 degrees)

Step 3: Find the angles formed by the diagonals
The diagonals bisect the angles of the rhombus:
- Therefore, ∠AOB = ∠AOD = 30 degrees (since ∠A = 60 degrees, and it is bisected)

Step 4: Use triangle properties
Let the diagonals AC and BD intersect at point O.
- We know that AO = OC and BO = OD (because diagonals bisect each other).

Step 5: Apply the sine rule in triangle AOB
In triangle AOB, we can use the sine function:
- We know that AB = 20 cm (hypotenuse), and we need to find OB (half of diagonal BD).
- Using the sine of angle AOB (30 degrees):

\( \sin(30^\circ) = \frac{OB}{AB} \)

Step 6: Substitute values
We know that:
- \(\sin(30^\circ) = \frac{1}{2}\)
- AB = 20 cm

Substituting these values into the equation gives us:

\( \frac{1}{2} = \frac{OB}{20} \)

Step 7: Solve for OB
Cross-multiplying gives:

\( OB = 20 \times \frac{1}{2} = 10 \text{ cm} \)

Step 8: Find the length of diagonal BD
Since OB = OD, the length of diagonal BD is:

\( BD = 2 \times OB = 2 \times 10 = 20 \text{ cm} \)

Step 9: Apply the cosine rule in triangle AOB
Now, we can find OA (half of diagonal AC) using the cosine function:
- Using the cosine of angle AOB (30 degrees):

\( \cos(30^\circ) = \frac{OA}{AB} \)

Step 10: Substitute values
We know that:
- \(\cos(30^\circ) = \frac{\sqrt{3}}{2}\)
- AB = 20 cm

Substituting these values into the equation gives us:

\( \frac{\sqrt{3}}{2} = \frac{OA}{20} \)

Step 11: Solve for OA
Cross-multiplying gives:

\( OA = 20 \times \frac{\sqrt{3}}{2} = 10\sqrt{3} \text{ cm} \)

Step 12: Find the length of diagonal AC
Since OA = OC, the length of diagonal AC is:

\( AC = 2 \times OA = 2 \times 10\sqrt{3} = 20\sqrt{3} \text{ cm} \)

Final Answer
The lengths of the diagonals are:
- BD = 20 cm
- AC = 20√3 cm