A wire of length 36m is to be cut into two pieces. One of the pieces is to be made into a square and the other into a circle. What should be the lengths of the two pieces, so that the combined area of the square and the circle is minimum?
To solve the problem of cutting a wire of length 36 meters into two pieces—one to form a square and the other to form a circle—such that the combined area of the square and the circle is minimized, we can follow these steps:
Step 1: Define Variables
Let:
- x = length of the wire used to form the square.
- y = length of the wire used to form the circle.
Since the total length of the wire is 36 meters, we have:
x+y=36
Step 2: Express the Areas
The area of the square As is given by:
As=(x4)2=x216
(The side of the square is x4 since the perimeter of the square is x.)
The area of the circle Ac is given by:
Ac=π(y2π)2=y24π
(The radius of the circle is y2π since the circumference of the circle is y.)
Step 3: Total Area
The total area A is the sum of the areas of the square and the circle:
A=As+Ac=x216+y24π
Step 4: Substitute for y
Using the equation y=36−x, we can substitute y in the total area equation:
A=x216+(36−x)24π
Step 5: Simplify the Area Function
Now, we simplify A:
A=x216+(36−x)24π
Expanding (36−x)2:
A=x216+1296−72x+x24π
Combining the terms:
A=x216+12964π−72x4π+x24π
A=(116+14π)x2−724πx+12964π
Step 6: Differentiate to Find Minimum Area
To find the minimum area, we differentiate A with respect to x and set it to zero:
dAdx=2(116+14π)x−724π=0
Solving for x:
2(116+14π)x=724π
x=724π⋅2(116+14π)
Step 7: Solve for x
Calculating x:
x=728(116+14π)=9116+14π
Step 8: Find y
Now, substitute x back to find y:
y=36−x
Step 9: Calculate the Lengths
After calculating x and y, we can find the lengths of the two pieces.
Final Answer
1. Length of the wire for the square: x
2. Length of the wire for the circle: y
Let:
- x = length of the wire used to form the square.
- y = length of the wire used to form the circle.
x+y=36
The area of the square As is given by:
As=(x4)2=x216
(The side of the square is x4 since the perimeter of the square is x.)
Ac=π(y2π)2=y24π
(The radius of the circle is y2π since the circumference of the circle is y.)
The total area A is the sum of the areas of the square and the circle:
A=As+Ac=x216+y24π
Using the equation y=36−x, we can substitute y in the total area equation:
A=x216+(36−x)24π
Now, we simplify A:
A=x216+(36−x)24π
Expanding (36−x)2:
A=x216+1296−72x+x24π
Combining the terms:
A=x216+12964π−72x4π+x24π
A=(116+14π)x2−724πx+12964π
To find the minimum area, we differentiate A with respect to x and set it to zero:
dAdx=2(116+14π)x−724π=0
Solving for x:
2(116+14π)x=724π
x=724π⋅2(116+14π)
Calculating x:
x=728(116+14π)=9116+14π
Now, substitute x back to find y:
y=36−x
After calculating x and y, we can find the lengths of the two pieces.
1. Length of the wire for the square: x
2. Length of the wire for the circle: y
Topper's Solved these Questions
Similar Questions
A wire of length 28 m is to be cut into two pieces. One of the pieces is to be made into a square and the other into a circle. What should be the length of the two pieces so that the combined area of the square and the circle is minimum?
View SolutionA wire of length 20m is to be cut into two pieces. One of the places will be bent into shape of a square and the other shape of an equilateral triangle. Where the wire should be cut so that the sum of the areas of the square and triangle is minimum?
View Solution
Knowledge Check
The side length of a square inscribed in a circle is 2. what is the area of the circle?
AπB√2πC2πD2√2π
A wire of length l is cut into two parts. One part is bent into a circle and the other into a square. Prove that the sum of the areas of the circle and the square is the least, if the radius of the circle is half of the side of the square.
View SolutionA wire of length 1212m is cut into 10 pieces of equal length. Find the length of each piece.
View SolutionA wire of length I is cut into three pleces. What Is the probability that the three pieces form a triangle ?
View SolutionA square is bisected into two equal triangle (see figure). If the length of BD is 16sqrt2 inches, what is the area of the square?
View SolutionA wire of length 2 units is cut into two parts which are bent respectively to from a square ofside c units and a circle of radius r units if the sum of the sum of the areas of the square and the circle so fromed is minimum then
View SolutionA square of the largest area is cut out of a circle. What % of the area of the circle is lost as trimmings ?
View SolutionA square is bisected into two triangles (see figure). If the length of BD is 16√2 inches, what is the area of the square?
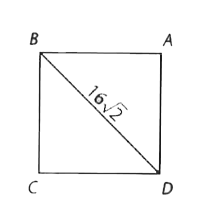
View Solution
