A square of the largest area is cut out of a circle. What % of the area of the circle is lost as trimmings ?
To solve the problem of finding the percentage of the area of the circle that is lost as trimmings when a square of the largest area is cut out, we can follow these steps:
Step 1: Understanding the Problem
We need to find the area of a square that can be inscribed in a circle and then determine what percentage of the circle's area is lost when this square is cut out.
Step 2: Area of the Circle
Let the radius of the circle be R. The area Ac of the circle is given by the formula:
Ac=πR2
Step 3: Area of the Square
The largest square that can be inscribed in a circle will have its diagonal equal to the diameter of the circle. The diameter of the circle is 2R.
Using the relationship between the side length s of the square and its diagonal d:
d=s√2
Setting the diagonal equal to the diameter of the circle:
s√2=2R
Solving for s:
s=2R√2=R√2
Now, we can find the area As of the square:
As=s2=(R√2)2=2R2
Step 4: Area Lost as Trimmings
The area lost when the square is cut out from the circle is the area of the square:
Area lost=As=2R2
Step 5: Percentage of Area Lost
To find the percentage of the area of the circle that is lost, we use the formula:
Percentage lost=(Area lostArea of circle)×100
Substituting the areas:
Percentage lost=(2R2πR2)×100
Simplifying:
Percentage lost=(2π)×100
Step 6: Final Calculation
Calculating the percentage:
Percentage lost=200π≈2003.14≈63.66%
Thus, the percentage of the area of the circle that is lost as trimmings when a square of the largest area is cut out is approximately 63.66%.
We need to find the area of a square that can be inscribed in a circle and then determine what percentage of the circle's area is lost when this square is cut out.
Let the radius of the circle be R. The area Ac of the circle is given by the formula:
Ac=πR2
The largest square that can be inscribed in a circle will have its diagonal equal to the diameter of the circle. The diameter of the circle is 2R.
d=s√2
Setting the diagonal equal to the diameter of the circle:
s√2=2R
Solving for s:
s=2R√2=R√2
As=s2=(R√2)2=2R2
The area lost when the square is cut out from the circle is the area of the square:
Area lost=As=2R2
To find the percentage of the area of the circle that is lost, we use the formula:
Percentage lost=(Area lostArea of circle)×100
Substituting the areas:
Percentage lost=(2R2πR2)×100
Simplifying:
Percentage lost=(2π)×100
Calculating the percentage:
Percentage lost=200π≈2003.14≈63.66%
Topper's Solved these Questions
- AREA RELATED TO CIRCLESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - AREA RELATED TO CIRCLESEXERCISE - Problems From NCERT /exemplar
25 Videos
- AREA RELATED TO CIRCLESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - AREA RELATED TO CIRCLESEXERCISE - Exercise 12 A
24 Videos
- ARITHMETIC PROGRESSIONBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - ARITHMETIC PROGRESSIONEXERCISE - Revision Exercise Long Answer Question
5 Videos
Similar Questions
Knowledge Check
The side length of a square inscribed in a circle is 2. what is the area of the circle?
AπB√2πC2πD2√2πA square is inscribed in a circle with area 9z. What is the area of the square?
A3√2B9√2C18D36What is the area of circle with a circumference of 10π?
A√10πB5πC25πD100π
If a square is inscribed in a circle, find the ratio of the areas of the circle and the square.
View SolutionIf a square is inscribed in a circle, what is the ratio of the areas of the circle and the square?
View Solution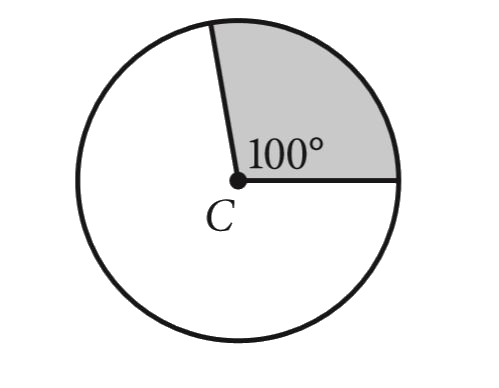
Point C is the center of the circle above. What fraction of the area of the circle is the area of the shaded region?
View SolutionA wire when bent in the form of square , encloses an area of 146 . 41 cm2 . If this wire is straightened and then bent to form a circle , what will be the area of the circle so formed ?
View SolutionWhat happen to area of circle, if its radius is doubled?
View Solution
