In Q. No. 14, write the sign of c .
To determine the sign of c in the polynomial y=ax2+bx+c where the parabola opens upwards, we can follow these steps:
1. Understand the Equation of the Parabola:
The given equation is y=ax2+bx+c. This represents a quadratic function.
2. Identify the Orientation of the Parabola:
The problem states that the parabola opens upwards. This occurs when the coefficient of x2 (which is a) is positive. Therefore, we have a>0.
3. Determine the Y-Intercept:
The y-intercept of the parabola can be found by substituting x=0 into the equation.
y=a(0)2+b(0)+c=c
This means that when x=0, the value of y is equal to c.
4. Analyze the Y-Intercept:
Since the parabola opens upwards, it means that as x moves away from 0 in both the positive and negative directions, y increases. Therefore, the point where the parabola intersects the y-axis (which is the point (0,c)) must be above the x-axis for the parabola to open upwards.
5. Conclusion about the Sign of c:
For the parabola to open upwards and intersect the y-axis at (0,c) above the x-axis, c must be greater than 0. Thus, we conclude that:
c>0
Final Answer:
The sign of c is positive (c>0).
The given equation is y=ax2+bx+c. This represents a quadratic function.
The problem states that the parabola opens upwards. This occurs when the coefficient of x2 (which is a) is positive. Therefore, we have a>0.
The y-intercept of the parabola can be found by substituting x=0 into the equation.
y=a(0)2+b(0)+c=c
This means that when x=0, the value of y is equal to c.
Since the parabola opens upwards, it means that as x moves away from 0 in both the positive and negative directions, y increases. Therefore, the point where the parabola intersects the y-axis (which is the point (0,c)) must be above the x-axis for the parabola to open upwards.
For the parabola to open upwards and intersect the y-axis at (0,c) above the x-axis, c must be greater than 0. Thus, we conclude that:
c>0
The sign of c is positive (c>0).
Topper's Solved these Questions
Similar Questions
Knowledge Check
The sign of a is positive. The sign of b is negative. If it can be determined, what is the sign of the mean of a and b?
APositiveBNegativeCBoth positive and negativeDCannot be determined from the given information.
Figures (a) and (b) show the field lines of a positive and negative point charge respectively.

(a) Give the signs of the potential difference VP−VQ,VB−VA.
(b) Give the sign of the potential energy difference of a small negative charge between the points Q and P, A and B.
(c) Give the sign of the work done by the field in moving a small positive charge from Q to P.
(d) Give the sign of the work done by the external agency in moving a small negative charge from B to A.
(e) Does the kinetic energy of a small negative charge increase or decrease in going from B to A?
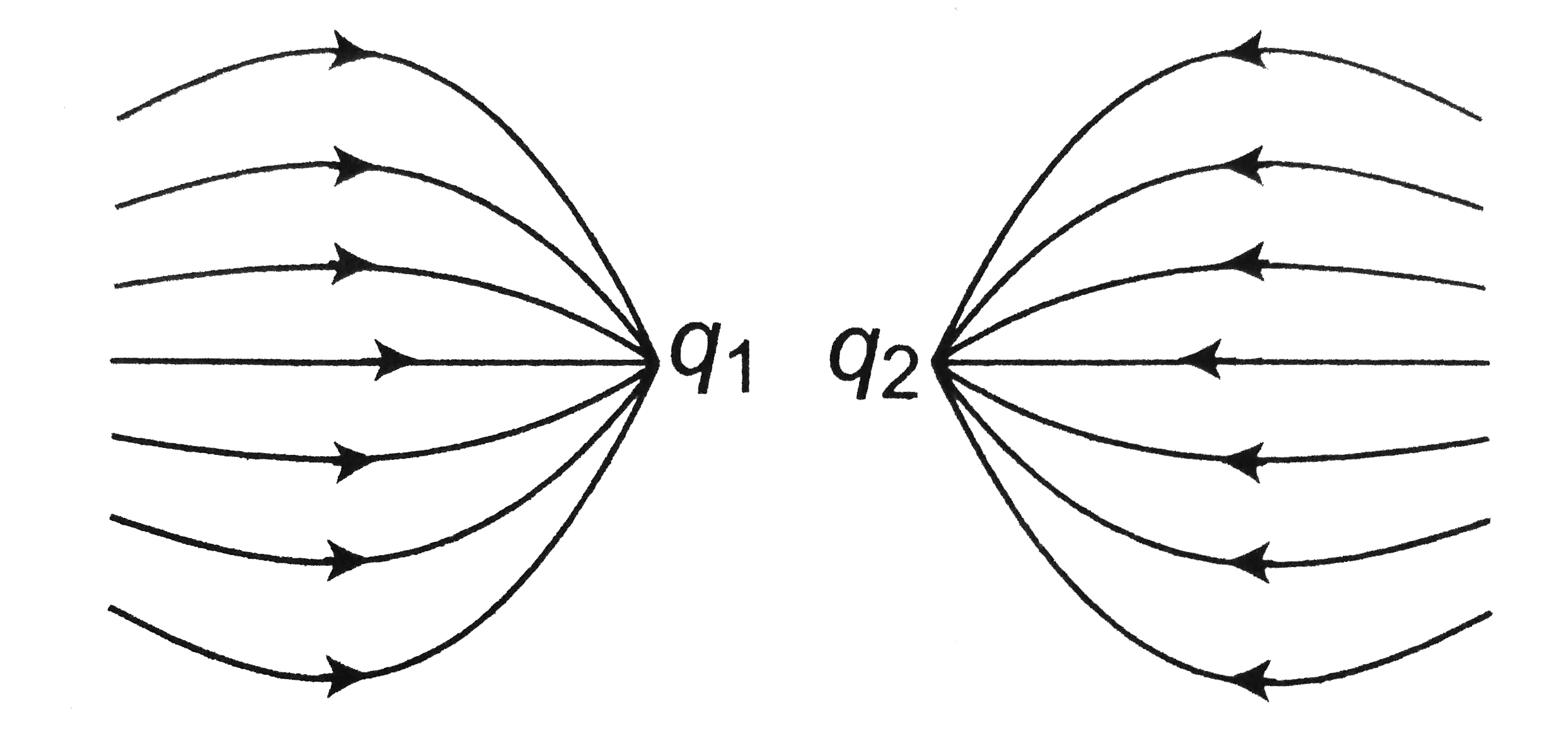
View SolutionThe given figure gives electric line of force due to two charges q1 and q2. What are the signs of the two charges ?
View SolutionConsider the situation shown in (figure) what are the signs of q1 and q2 ? If the lines are drawn in proportion to the charge, what is the ratio q1q2 ?

View SolutionThe figure is a plot of lines of force due to two charges q1andq2. Find out the sign of charges.

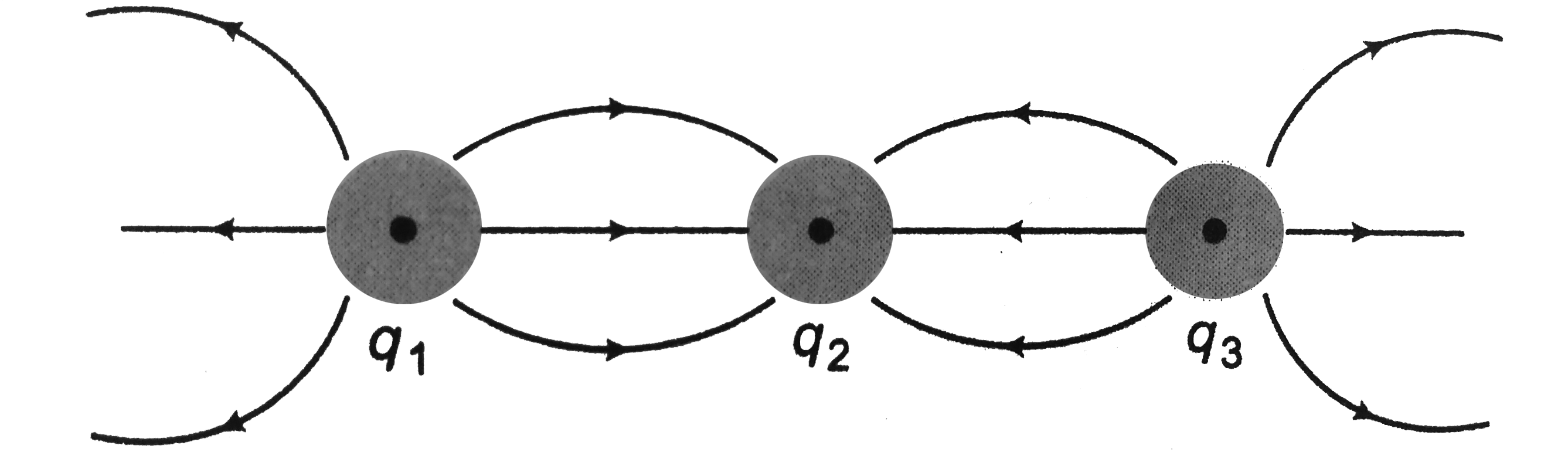
View SolutionFigure shows some of the electric field lines due to three point charges q,q2 and q3 of equal magnitude. What are the signs of each of the three charges?
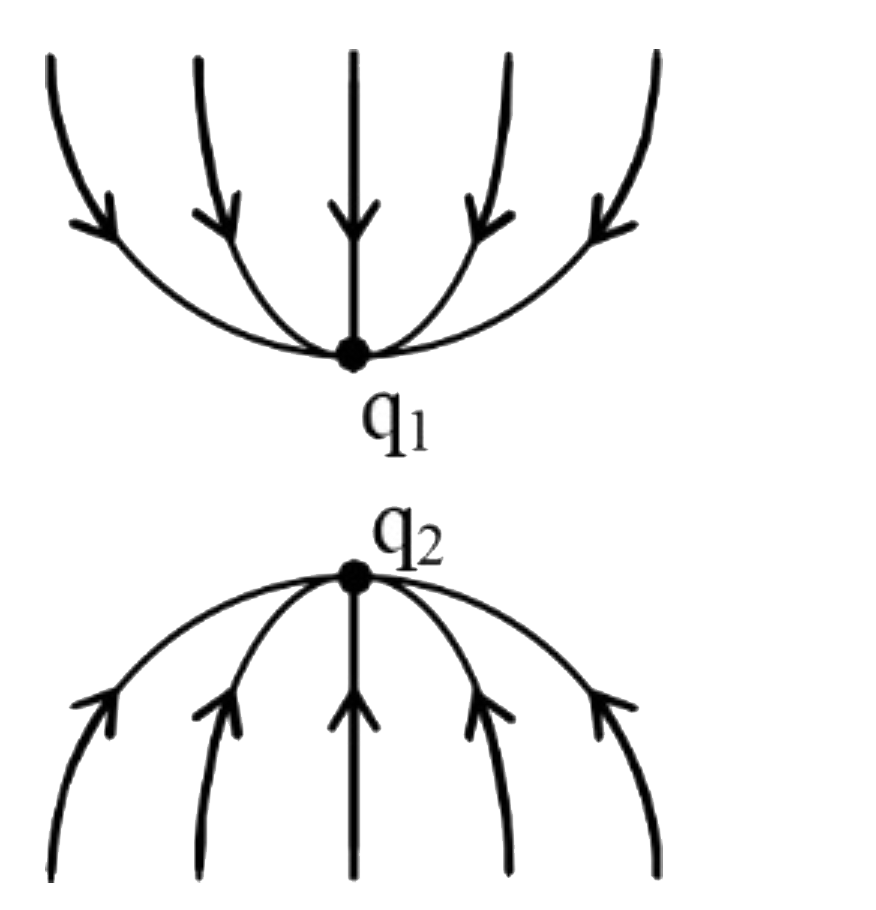
View SolutionIn the adjoining figure, the electric field lines for charges q1andq2 are shown. Identify the sign of the charges.
View SolutionThree charges are placed as shown in fig. the magnitude of q1 is 2.00μC, but its sign is unknown. Value of charge q2 is unknown and the value of the charge q3 is +4.00μC, and the net force on q3 is entirely in the negative x-direction
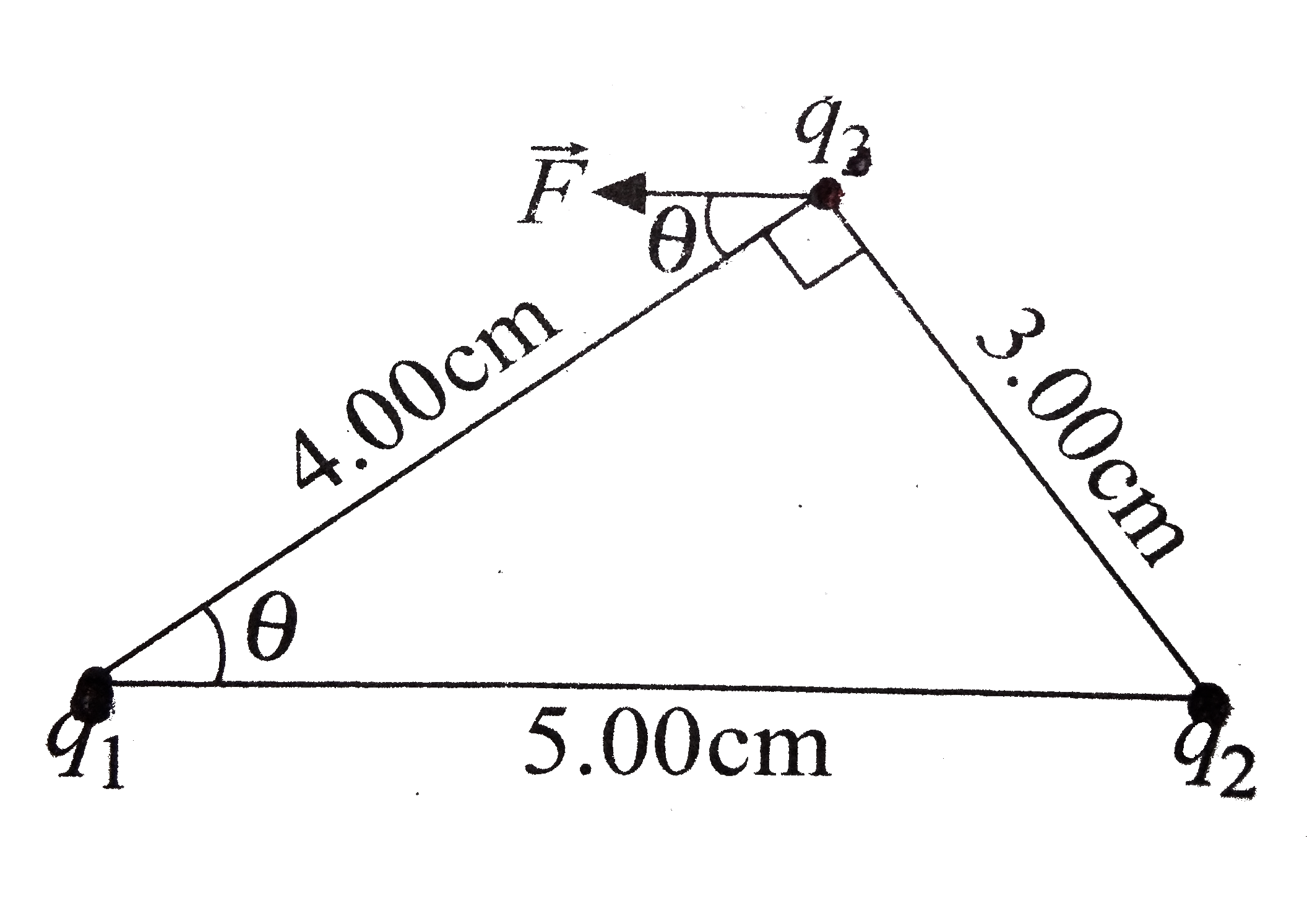
As per the condition given in the problem, the sign of q1 and q2 will be
View Solution
