In Figure, express x in terms of a, b and c.
To express x in terms of a,b, and c, we can follow these steps based on the information provided in the question and the video transcript.
1. Identify the Given Ratios: From the problem, we know that:
QtPr=QrQs
This can be rearranged to:
QtQr=PrQs
Let's denote this as Equation (1).
2. Use the Given Angles: We are given that:
∠1=∠2
This implies that the triangles involving these angles have proportional sides.
3. Apply the Angle-Side Relationship: Since ∠1=∠2, we can conclude that:
PRPQ=QTQR
This can be rearranged to:
PQQT=QRPR
Let's denote this as Equation (2).
4. Establish Similarity of Triangles: From Equations (1) and (2), we can state that:
PQQT=QSQR
This indicates that triangles PQS and TQR are similar by the Side-Angle-Side (SAS) criterion.
5. Express x: Since the triangles are similar, we can express x in terms of a,b, and c using the ratios of the corresponding sides:
x=k⋅a
where k is a proportionality constant that can be determined based on the ratios of the sides.
6. Final Expression: Assuming k can be expressed in terms of b and c, we can write:
x=bc⋅a
Final Answer:
Thus, the expression for x in terms of a,b, and c is:
x=bc⋅a
QtPr=QrQs
This can be rearranged to:
QtQr=PrQs
Let's denote this as Equation (1).
∠1=∠2
This implies that the triangles involving these angles have proportional sides.
PRPQ=QTQR
This can be rearranged to:
PQQT=QRPR
Let's denote this as Equation (2).
PQQT=QSQR
This indicates that triangles PQS and TQR are similar by the Side-Angle-Side (SAS) criterion.
x=k⋅a
where k is a proportionality constant that can be determined based on the ratios of the sides.
x=bc⋅a
Thus, the expression for x in terms of a,b, and c is:
x=bc⋅a
Topper's Solved these Questions
Similar Questions
Knowledge Check
If V=13Bh, what is h expressed in terms of B and V?
A13BVBV3BC3VBD3VBIn the formula 23a−45b=54c , what is the correct expression of a in terms of b and c?
A40bc3(16b+25c)B40bc3(16b+25c)C40bc3(25b+16c)D40bc3(25b−16c)Which of the following equations expresses c in terms of a for all real numbers a, b and c such that a3=b and b2=c ?
Ac=a6Bc=a5Cc=2a3Dc=12a
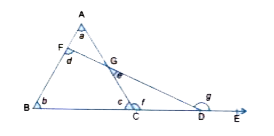
Use the given figure to express :
(i) a in terms of b and f,
(ii) e in terms of f and g,
(iii) d in terms of a and e,
(iv) c in terms of e and g.
View SolutionLet a and b be given non-zero and non-collinear vectors, such that c×a=b−c. Express c in terms for a, b and aXb.
View SolutionIn Figure, what is y in terms of x ? (a)32x (b) 43x (c) x (d) 34x
View SolutionGiven log10x=aandlog10y=b.
(i) Write down 10a−1 in terms of x.
(ii) Write down 102b in terms of y.
(iii) If log10P=2a−b, express P in terms of x and y.
View SolutionWrite down the algebraic expressions whose terms are :
3a,−4b,7c
View Solution
