In the adjoining figure, if is the bisector of if BD=4cm ,DC=3cm and AB=6cm , what is ?
To solve the problem, we will use the Angle Bisector Theorem, which states that if a point D lies on the side BC of triangle ABC, such that AD is the bisector of angle A, then:
BDDC=ABAC
Given:
- BD = 4 cm
- DC = 3 cm
- AB = 6 cm
- We need to find AC.
1. Set up the ratio using the Angle Bisector Theorem:
According to the theorem, we can write:
BDDC=ABAC
Substituting the known values:
43=6AC
2. Cross-multiply to solve for AC:
Cross-multiplying gives us:
4⋅AC=6⋅3
Simplifying the right side:
4⋅AC=18
3. Isolate AC:
To find AC, divide both sides by 4:
AC=184
Simplifying this fraction:
AC=4.5 cm
Final Answer:
Thus, the length of AC is 4.5 cm.
- BD = 4 cm
- DC = 3 cm
- AB = 6 cm
- We need to find AC.
According to the theorem, we can write:
BDDC=ABAC
Substituting the known values:
43=6AC
Cross-multiplying gives us:
4⋅AC=6⋅3
Simplifying the right side:
4⋅AC=18
To find AC, divide both sides by 4:
AC=184
Simplifying this fraction:
AC=4.5 cm
Thus, the length of AC is 4.5 cm.
Topper's Solved these Questions
Similar Questions
In the given figure AD is the bisector of ∠A. If BD= 4 cm , DC = 3 cm and AB = 6cm . Find AC.

View SolutionIn the adjoining figure, O is the centre of the circle and AB is its diameter. If AC=8 cm and BC= 6cm, then find the radius of the circle.

View SolutionIn the adjoining figure, BD is the diameter of the circle which bisects the chord AC at point E. If AC=8cm, BE=2cm, then find the radius of the circle.

View SolutionIn a △ABC , AD is the bisector of ∠A , meeting side BC at D . (i)IfAB=10cm , AC=14cm and BC=6cm , find BD and DC (ii)IfAC=4.2cm , DC=6cm and BC=10cm , find AB . (iii)IfAB=5.6cm , AC=6cm and DC=3cm , find BC .
View SolutionIn the adjoining figure, DE//BC and D divides AB in the ratio 2 : 3. Find DE, if BC = 7.5 cm.
View SolutionIn the adjoining figure, ABC is a triangle right-angled at vertex A and AD is altitude.

If BD = 3.6 cm and CD = 6.4 cm, find the length of AD.
View SolutionIn the adjoining figure, AB=8cm,DM=6cmandBC=6cm. Find the length of DN

View SolutionIn the adjoining figure, ABC is a triangle and D is any point in its interior. Show that BD+DC<AB+AC.
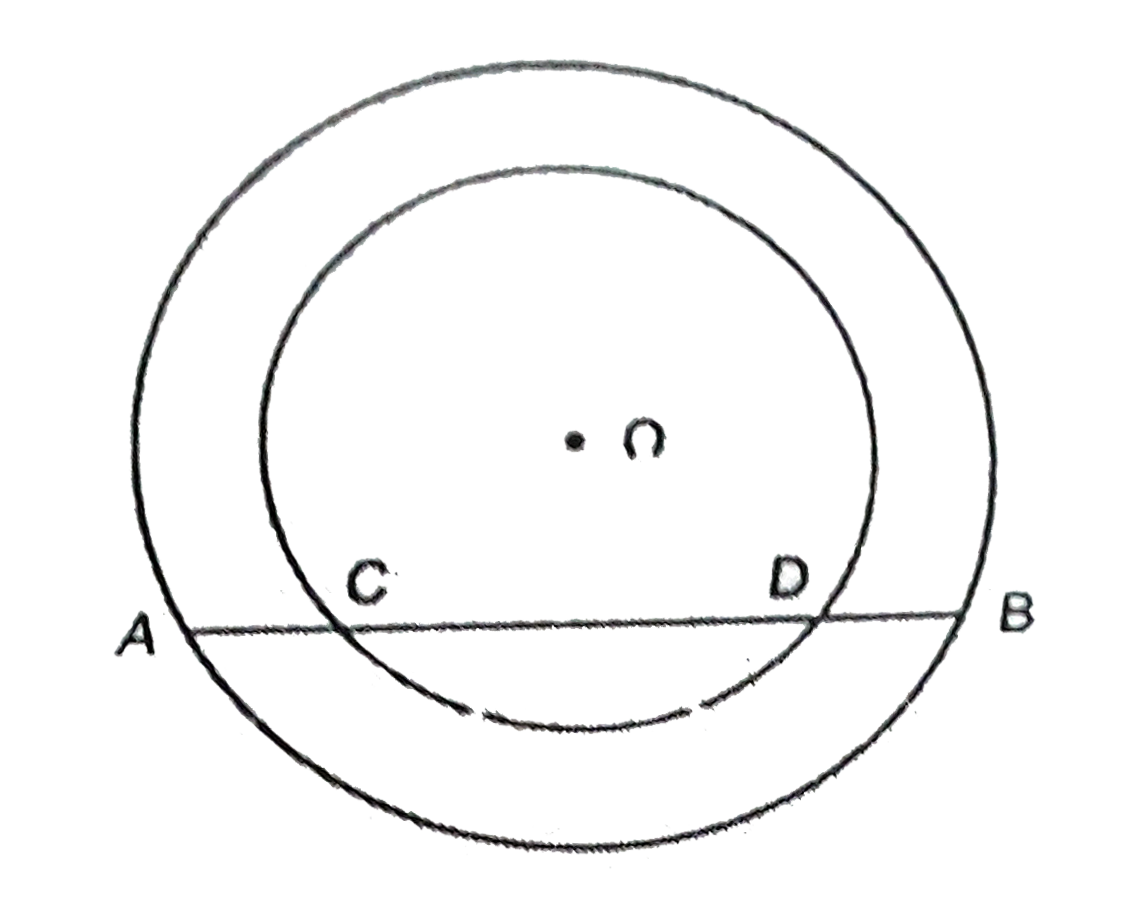
View SolutionIn the adjoining figure,O is the centre of two concentric circles. The chord AB of larger circle intersects the smaller circle at C and D.
(i) Find AC:BD.
(ii) If AC=2cm, then find the length of BD.
View SolutionIn the given figure, AB and DE are perpendicular to BC. If AB = 6cm, DE = 4cm and AC = 15cm.

(iii) Find the ratio of the area of ΔABC : area of ΔDEC.
View Solution
