State AA similarity criterion.
Step-by-Step Solution for AA Similarity Criterion
1. Understanding AA Similarity Criterion: The AA (Angle-Angle) similarity criterion states that if in two triangles, two angles of one triangle are equal to two angles of another triangle, then the two triangles are similar.
2. Let’s Define the Triangles: Consider two triangles, Triangle ABC and Triangle DEF. We need to show that if ∠A = ∠D and ∠B = ∠E, then Triangle ABC is similar to Triangle DEF.
3. Using the Angle Sum Property: According to the angle sum property of triangles, the sum of the angles in a triangle is always 180 degrees. Therefore, for Triangle ABC:
∠A+∠B+∠C=180∘
And for Triangle DEF:
∠D+∠E+∠F=180∘
4. Substituting Known Angles: Since we know that ∠A = ∠D and ∠B = ∠E, we can substitute these values into the angle sum equations:
- For Triangle ABC:
∠D+∠E+∠C=180∘
- For Triangle DEF:
∠D+∠E+∠F=180∘
5. Equating the Angles: Now, we can equate the two equations by substituting (∠D + ∠E) from Triangle DEF into the equation for Triangle ABC:
180∘−∠C=180∘−∠F
6. Conclusion About the Third Angles: From the above equation, we can conclude that:
∠C=∠F
This shows that the third angles of both triangles are also equal.
7. Final Statement: Since all three angles of Triangle ABC are equal to the corresponding angles of Triangle DEF, we can conclude that Triangle ABC is similar to Triangle DEF by the AA similarity criterion.
∠A+∠B+∠C=180∘
And for Triangle DEF:
∠D+∠E+∠F=180∘
- For Triangle ABC:
∠D+∠E+∠C=180∘
- For Triangle DEF:
∠D+∠E+∠F=180∘
180∘−∠C=180∘−∠F
∠C=∠F
This shows that the third angles of both triangles are also equal.
Topper's Solved these Questions
Similar Questions
State SAS similarity criterion.
View SolutionState SSS similarity criterion.
View SolutionState which pairs of triangles in Figure are similar. Write the similarity criterion used by you for answering the question and also write the pairs of similar triangles in the symbolic form:
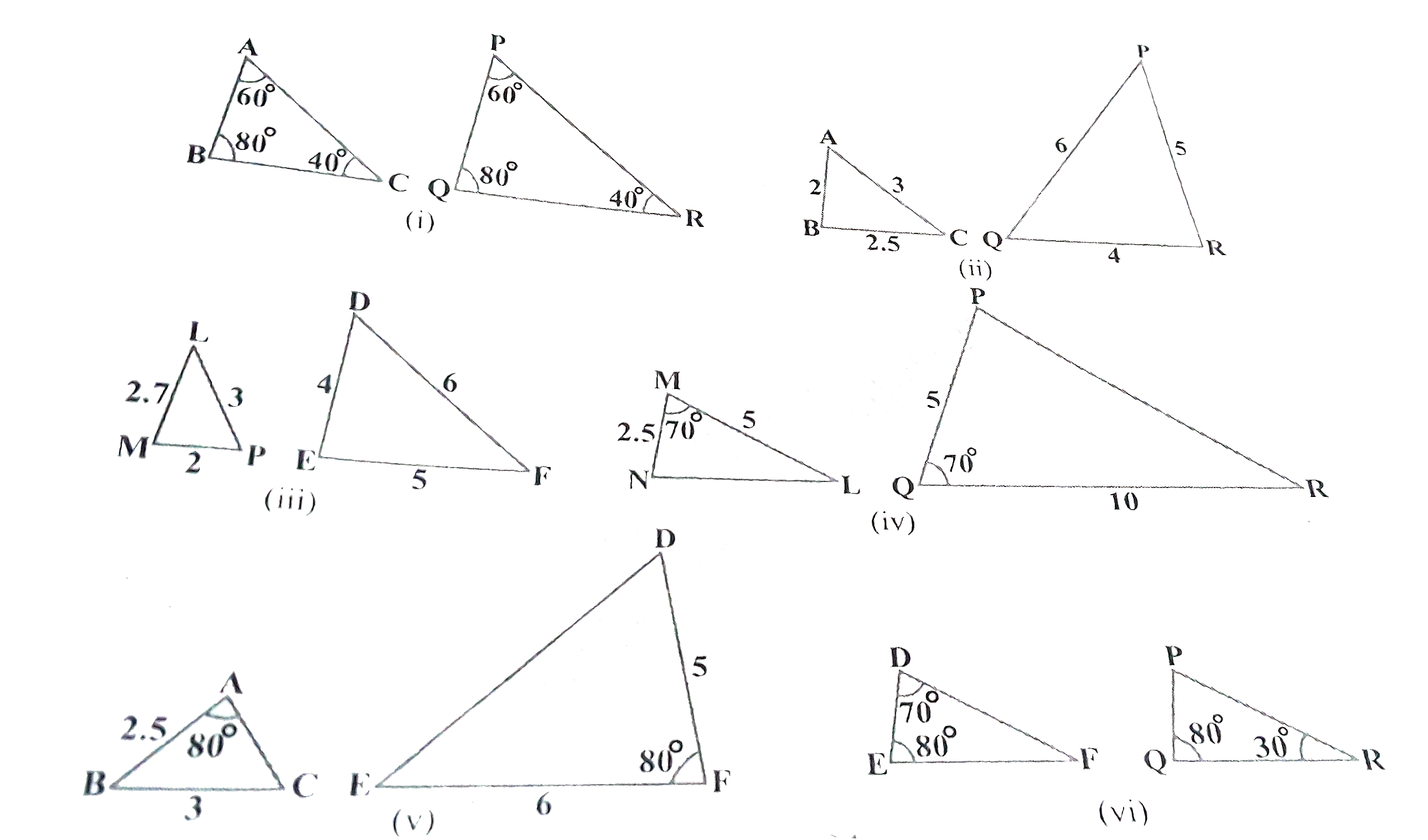
View SolutionState which pairs of triangles in Figure are similar. Write the similarity criterion used by you for answering the question and also write the pairs of similar triangles in the symbolic form:
View SolutionDiagonals AC and BD of a trapezium ABCD with AB || DC intersect each other at the point O. Using a similarity criterion for two triangles, show that OAOC=OBOD
View SolutionDiagonals AC and BD of a trapezium ABCD with AB,DC intersect each other at the point O . Using similarity criterion for two triangles, show that OAOC=OBOD .
View SolutionParthenocarpy nd apomixis have been observed in some plants. Give an example of each. State a similarity and a difference oberved between the two processes.
View Solution
State four similarities between the ideologies of Nazism and Fascism.
View SolutionWhich of the following states the similarity between DNA and RNA, :
View SolutionState two similarities and two differences between respiration and burning.
View Solution
