In Fig. 4.241, DEBC and AD=12BD . If BC=4.5cm , find DE . (FIGURE)
To solve the problem step by step, we will use the properties of similar triangles and the given information.
1. Identify the Given Information:
- We know that DE is parallel to BC.
- We are given that AD=12BD.
- We also know that BC=4.5cm.
2. Set Up the Relationship:
- Let AD=x. Then, since AD=12BD, we can express BD as:
BD=2x
- Therefore, the entire length AB can be expressed as:
AB=AD+BD=x+2x=3x
3. Use the Properties of Similar Triangles:
- Since DE is parallel to BC, by the Basic Proportionality Theorem (or Thales' theorem), we have:
ADAB=DEBC
- Substituting the values we have:
x3x=DE4.5
4. Simplify the Equation:
- The left side simplifies to:
13=DE4.5
5. Cross-Multiply to Solve for DE:
- Cross-multiplying gives us:
DE=13×4.5
6. Calculate DE:
- Performing the multiplication:
DE=4.53=1.5cm
Final Answer:
Thus, the length of DE is 1.5cm.
---
- We know that DE is parallel to BC.
- We are given that AD=12BD.
- We also know that BC=4.5cm.
- Let AD=x. Then, since AD=12BD, we can express BD as:
BD=2x
- Therefore, the entire length AB can be expressed as:
AB=AD+BD=x+2x=3x
- Since DE is parallel to BC, by the Basic Proportionality Theorem (or Thales' theorem), we have:
ADAB=DEBC
- Substituting the values we have:
x3x=DE4.5
- The left side simplifies to:
13=DE4.5
- Cross-multiplying gives us:
DE=13×4.5
- Performing the multiplication:
DE=4.53=1.5cm
Thus, the length of DE is 1.5cm.
Topper's Solved these Questions
Similar Questions
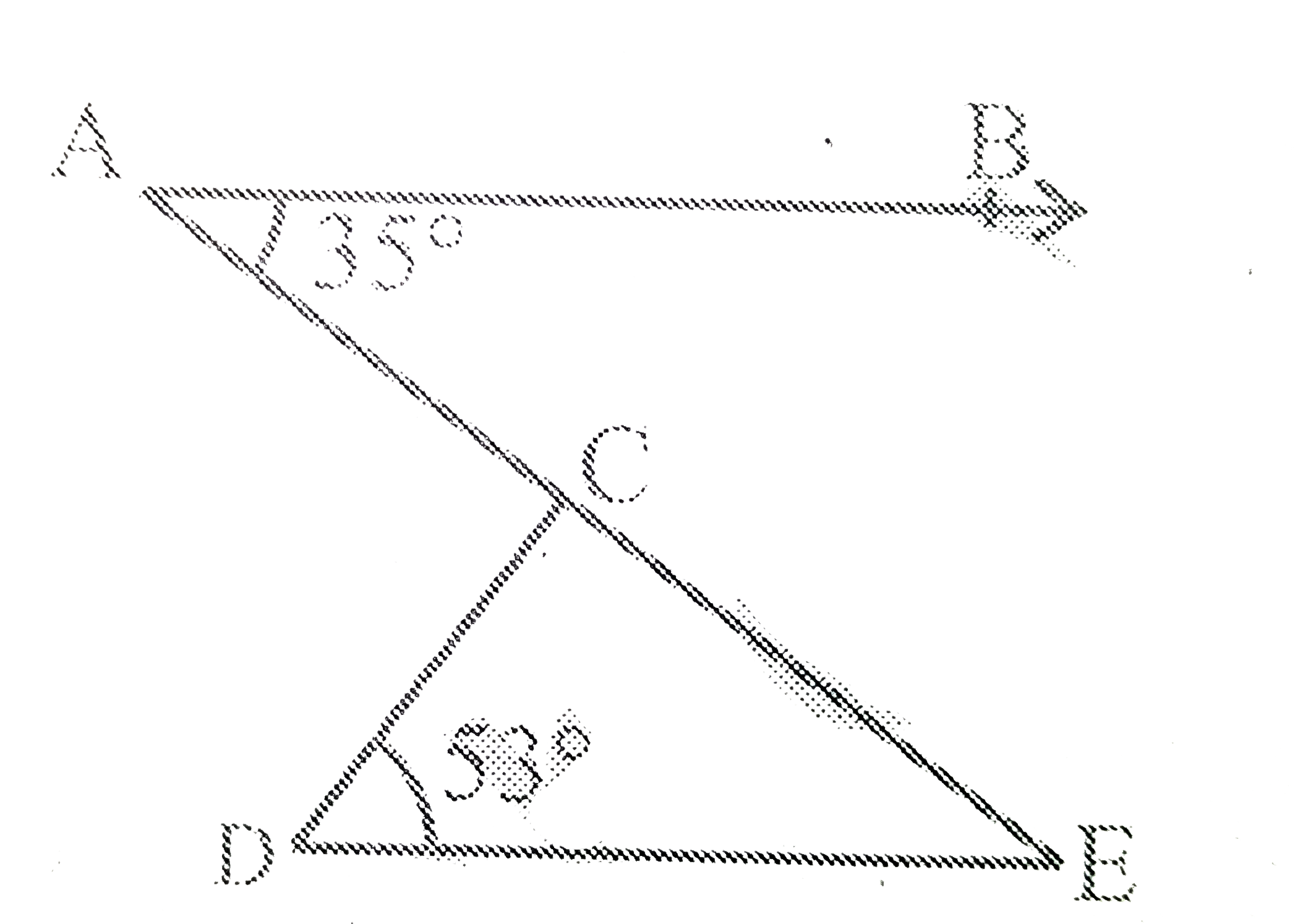
In Fig. 6.41, if AB∣∣DE,∠BAC=35∘ and ∠CDE=53∘, find ∠DCE.
View SolutionIn Fig. 4.140, ∠ABC=90o and BD⊥AC . If AB=5.7cm , BD=3.8 cm and CD=5.4cm , find BC . (FIGURE)
View SolutionIn Fig. 4.125, FEC≅GBD and ∠1=∠2 . Prove that ADEABC . (FIGURE)
View SolutionIn Fig. 4.143, ∠A=∠CED , prove that CAB∼CED . Also, find the value of x . (FIGURE)
View SolutionIn Fig. 4.246, if PBCF and DPEF , then ADDE= (FIGURE) 34 (b) 13 (c) 14 (d) 23
View SolutionIn Fig. 4.145, if AB⊥BC , DC⊥BC and DE⊥AC , prove that CED∼ABC . (FIGURE)
View SolutionIn Figure, if AB ∣∣DE, ∠BAC=350and ∠CDE=530, find ∠DCE.
View SolutionIn Fig. 4.178, DE∥BC (FIGURE) (i) If DE=4cm , BC=6cm and Area (ADE)=16 cm2 , find the area of ABC . (ii) If DE=4cm, BC=8cm and Area (ADE)=25 cm2 , find the area of ABC . (iii) If DE:BC=3:5 . Calculate the ratio of the areas of ADE and the trapezium BCED .
View SolutionIn Fig. 4.42, AD is the bisector of ∠BAC . If AB=10cm . AC=14cm and BC=6cm , find BD and DC . (FIGURE)
View SolutionIn Figure if ∠ADE=∠B show that ADE~ABC . If AD=3.8cm , AE=3.6cm , BE=2.1cm and BC=4.2cm , find DE.
View Solution
