Question

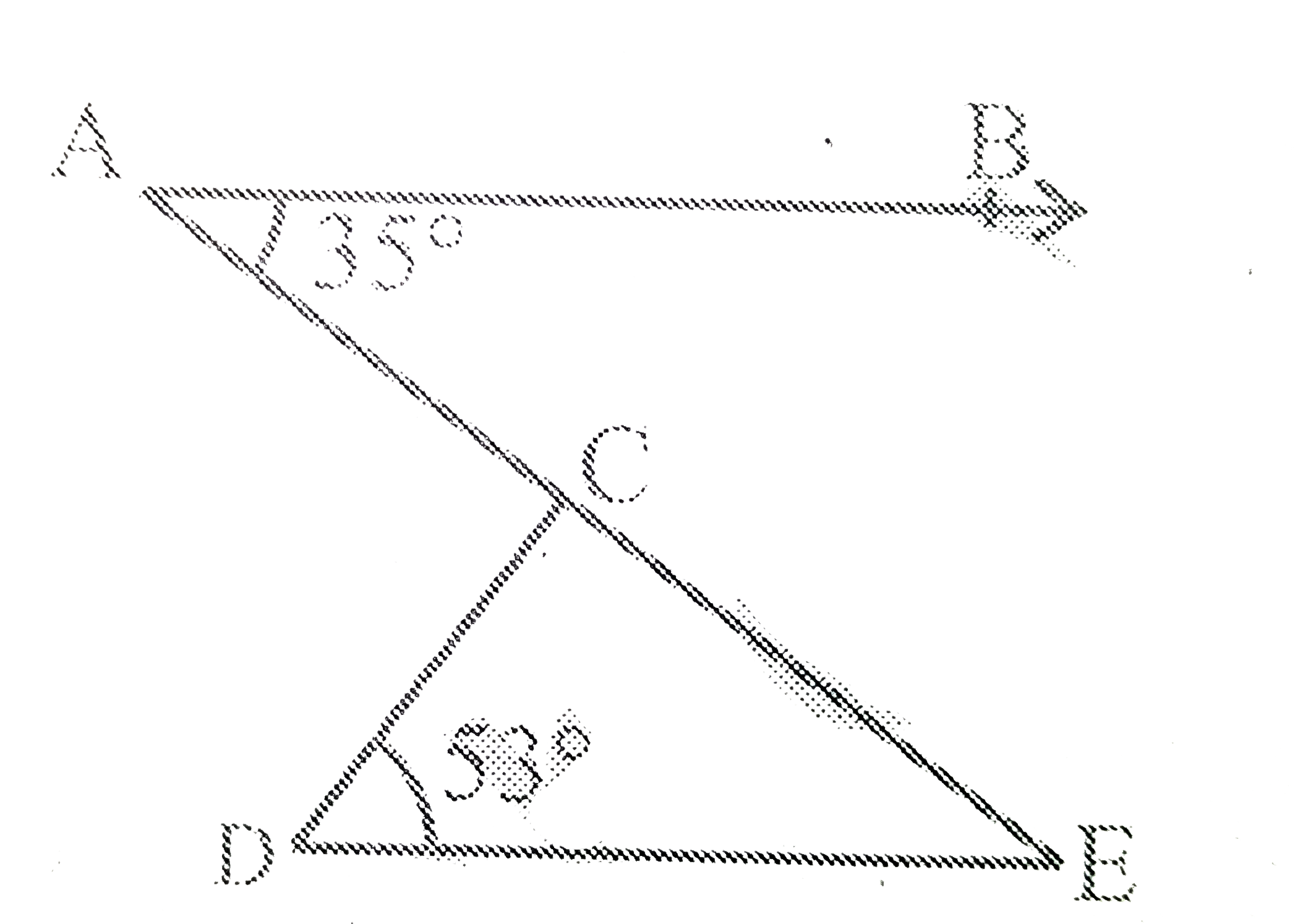
In Figure, if $AB\mid \mid DE,\angle BAC={35}^{0}and\angle CDE={53}^0,$
find $\angle DCE\stackrel{.}{}$

Explanation

To solve the problem, we will follow these steps:

Step 1: Identify the given information
We are given that:
- \( AB \parallel DE \)
- \( \angle BAC = 35^\circ \)
- \( \angle CDE = 53^\circ \)

Step 2: Use the property of alternate angles
Since \( AB \) is parallel to \( DE \) and \( AE \) is a transversal, we can use the property of alternate angles. This tells us that:
\( \angle BAE = \angle CED \)
Thus, we can conclude:
\( \angle CED = 35^\circ \)

Step 3: Apply the angle sum property in triangle CDE
In triangle \( CDE \), the sum of the interior angles is \( 180^\circ \). Therefore, we can write:
\( \angle CDE + \angle CED + \angle DCE = 180^\circ \)
Substituting the known angles:
\( 53^\circ + 35^\circ + \angle DCE = 180^\circ \)

Step 4: Simplify the equation
Now, we can simplify:
\( 88^\circ + \angle DCE = 180^\circ \)

Step 5: Solve for angle DCE
To find \( \angle DCE \), we subtract \( 88^\circ \) from \( 180^\circ \):
\( \angle DCE = 180^\circ - 88^\circ = 92^\circ \)

Final Answer
Thus, the measure of angle \( DCE \) is:
\( \angle DCE = 92^\circ \)

---