Question

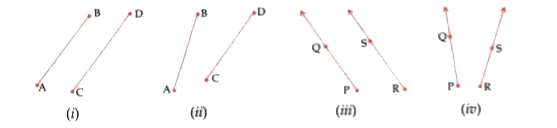
Which pair of lines in
Fig. are parallel? Given reasons.

Explanation

To determine which pair of lines in the given figure are parallel, we will analyze the angles provided and apply the properties of supplementary angles.

1. Identify the Angles:
- We have the following angles:
- Angle A = 115°
- Angle B = 116°
- Angle C = 115°
- Angle D = 65°

2. Check for Supplementary Angles:
- We will first check if angle A and angle D are supplementary:
- Angle A + Angle D = 115° + 65° = 180°
- Since the sum is 180°, angle A and angle D are supplementary.

3. Conclusion for the First Pair:
- According to the properties of parallel lines, if two angles are supplementary, then the lines are parallel.
- Therefore, line AB is parallel to line CD (AB || CD).

4. Check Another Pair:
- Now, we will check if angle A and angle B are supplementary:
- Angle A + Angle B = 115° + 65° = 180°
- Since this sum is also 180°, angle A and angle B are supplementary.

5. Conclusion for the Second Pair:
- Thus, line AD is parallel to line BC (AD || BC).

Final Answer:
- The pairs of parallel lines are:
- AB || CD (because angle A + angle D = 180°)
- AD || BC (because angle A + angle B = 180°)