Explain how this figure is a trapezium. Which of its two sides are parallel? (Fig 3.32)
To determine how the given figure is a trapezium and identify the parallel sides, follow these steps:
1. Identify the Angles: In the given figure, we have two angles: angle M = 100 degrees and angle L = 80 degrees.
2. Sum of Angles: Calculate the sum of these two angles:
Angle M+Angle L=100∘+80∘=180∘
3. Understanding Co-Interior Angles: In a trapezium, if a pair of co-interior angles (angles on the same side of a transversal) sum up to 180 degrees, then the lines that form these angles are parallel.
4. Identify the Transversal: Here, line ML acts as the transversal between the two lines NM and KL.
5. Conclusion on Parallel Lines: Since the sum of the co-interior angles (angle M and angle L) is 180 degrees, we can conclude that the lines NM and KL are parallel. Therefore, we write:
Line NM∥Line KL
6. Final Statement: Since one pair of opposite sides (NM and KL) are parallel, we can conclude that the figure is a trapezium.
Final Answer:
The figure is a trapezium because one pair of opposite sides, NM and KL, are parallel.
---
Angle M+Angle L=100∘+80∘=180∘
Line NM∥Line KL
The figure is a trapezium because one pair of opposite sides, NM and KL, are parallel.
Topper's Solved these Questions
- UNDERSTANDING QUADRILATERALSBOOK - NCERT ENGLISHCHAPTER - UNDERSTANDING QUADRILATERALSEXERCISE - EXERCISE 3.2
6 Videos
- SQUARES AND SQUARE ROOTSBOOK - NCERT ENGLISHCHAPTER - SQUARES AND SQUARE ROOTSEXERCISE - EXERCISE 6.4
9 Videos
- VISUALISING SOLID SHAPESBOOK - NCERT ENGLISHCHAPTER - VISUALISING SOLID SHAPESEXERCISE - EXERCISE 10.3
8 Videos
Similar Questions
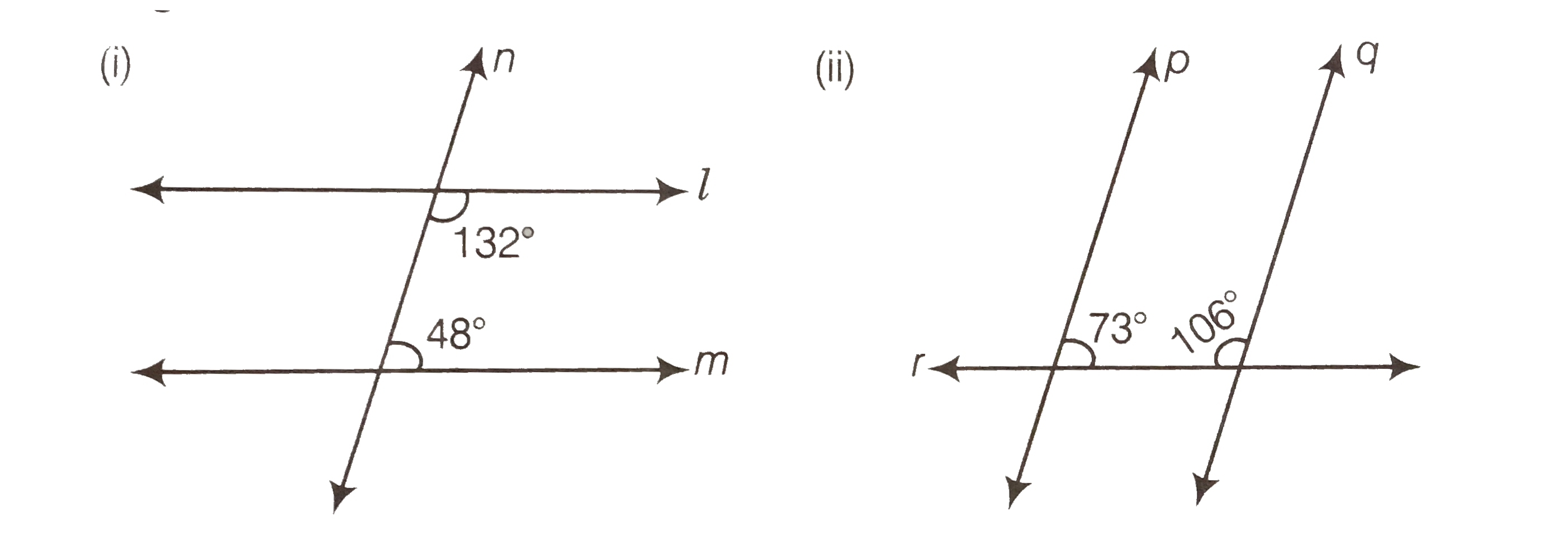
In the figure, which of the two lines are parallel and why ?
View SolutionIn the adjoining figure, explain :
(i) which side is the greatest side ?
(ii) which of two sides are equal ?
(iii) which is the smallest side of ΔAQS ?

View SolutionWhich pair of lines in Fig. are parallel? Given reasons.
View SolutionFind the height of a trapezium, the sum of the lengths of whose base (parallel sides) is 60cm and whose area is 600 cm2.
View SolutionIf a triangle is inscribed in an ellipse and two of its sides are parallel to the given straight lines, then prove that the third side touches the fixed ellipse.
View SolutionThe shape of the top surface of a table is a trapezium. Find its area if its parallel sides are 1 m and 1.2 m and perpendicular distance between them is 0.8 m.
View SolutionIn the given figure ABCD is a trapezium, P is the mid-point of side AD and PR||AB||DC.
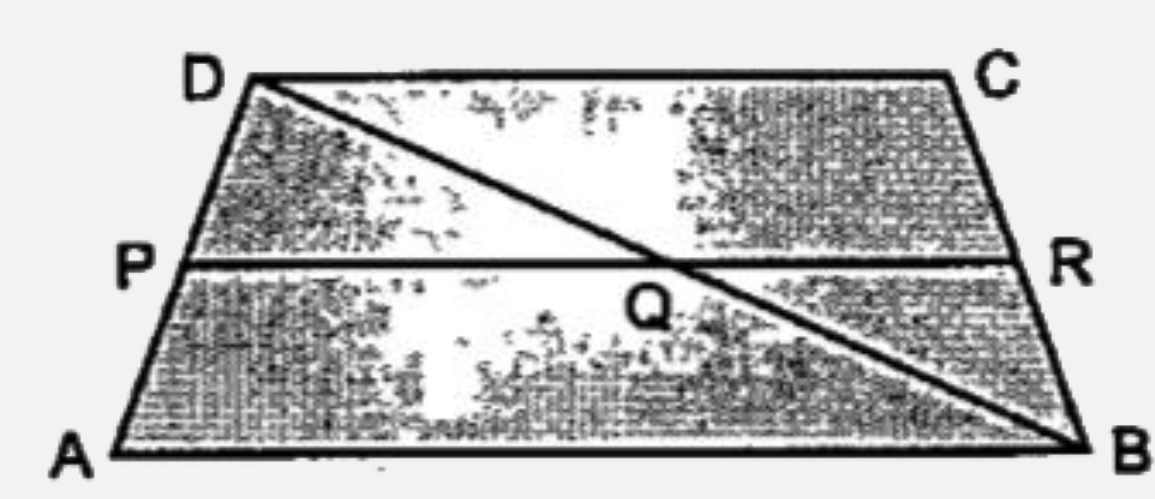
Prove that R is the mid-point of side BC
View SolutionIf two opposite sides of a cyclic quadrilateral are equal, then the other two sides are parallel.
View SolutionIn Fig.86, state which lines are parallel and why?
View SolutionMohan wants to buy a trapezium shaped field. Its side along the river is parallel to and twice the side along the road. If the area of this field is 10500 m2 and the perpendicular distance between the two parallel sides is 100 m, find the length of the side along the river.
View Solution
