In Figure, if AB||HF and DE||FG , then the measure of ∠FDE is (a) 1080 (b) 800 (c) 1000 (d) 900
To solve the problem step-by-step, we will use the properties of parallel lines and angles.
Step 1: Identify the Given Information
We know that:
- Lines AB and HF are parallel.
- Lines DE and FG are parallel.
- The measure of angle GHF is 28∘.
- The measure of angle EDB is 72∘.
Step 2: Use Corresponding Angles
Since AB∥HF, the angle GHF (which is 28∘) is a corresponding angle to angle FDA. Therefore, we can write:
∠FDA=∠GHF=28∘
Step 3: Use the Sum of Angles in a Straight Line
Next, we consider the angles around point D. The angles EDB, FDE, and FDA form a straight line. Thus, we can write the equation:
∠EDB+∠FDE+∠FDA=180∘
Step 4: Substitute Known Values
Now we substitute the known values into the equation:
72∘+∠FDE+28∘=180∘
Step 5: Simplify the Equation
Combine the known angles:
100∘+∠FDE=180∘
Step 6: Solve for ∠FDE
Now, isolate ∠FDE:
∠FDE=180∘−100∘=80∘
Conclusion
Thus, the measure of angle FDE is:
∠FDE=80∘
The correct answer is option (b) 80∘.
---
We know that:
- Lines AB and HF are parallel.
- Lines DE and FG are parallel.
- The measure of angle GHF is 28∘.
- The measure of angle EDB is 72∘.
Since AB∥HF, the angle GHF (which is 28∘) is a corresponding angle to angle FDA. Therefore, we can write:
∠FDA=∠GHF=28∘
Next, we consider the angles around point D. The angles EDB, FDE, and FDA form a straight line. Thus, we can write the equation:
∠EDB+∠FDE+∠FDA=180∘
Now we substitute the known values into the equation:
72∘+∠FDE+28∘=180∘
Combine the known angles:
100∘+∠FDE=180∘
Now, isolate ∠FDE:
∠FDE=180∘−100∘=80∘
Thus, the measure of angle FDE is:
∠FDE=80∘
Topper's Solved these Questions
Similar Questions
In Figure, BD=DC and ∠DBC=250 find the measure of ∠BAC
View SolutionIn Figure, If AB||CD and CD ||EF, Find ∠ACE.
View SolutionIn Figure, AB||CF and BC||ED . Prove that ∠ABC= ∠FDE
View SolutionIn Figure, AB∣∣CD and ∠F=30∘ . Find ∠ECD.
View SolutionIn Figure, AB|| CD and EF||DQ Determine ∠PDQ, ∠AED and ∠DEF
View SolutionIn Figure, PQ∣∣RS, ∠AEF=950, ∠BHS=1100 and ∠ABC=x0. Then the value of x is (a)150 (b) 250 (c) 700 (d) 350
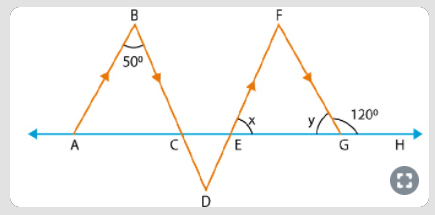
View SolutionIn Figure, if AB∣∣DF and BD∣∣FG such that ∠FGH=120∘ and ∠B=50∘, find x and y.
View SolutionIn Figure, ABCD and AEFG are parallelograms. If ∠C=550, what is the measure of ∠F?
View SolutionIn Figure, lines AB, CD and EF intersect at O. Find the measures of ∠AOC, ∠COF, ∠DOE and ∠BOF .
View SolutionIn Figure ABCD and AEFD are two parallelograms. Prove that: PE=FQ
View Solution