Question

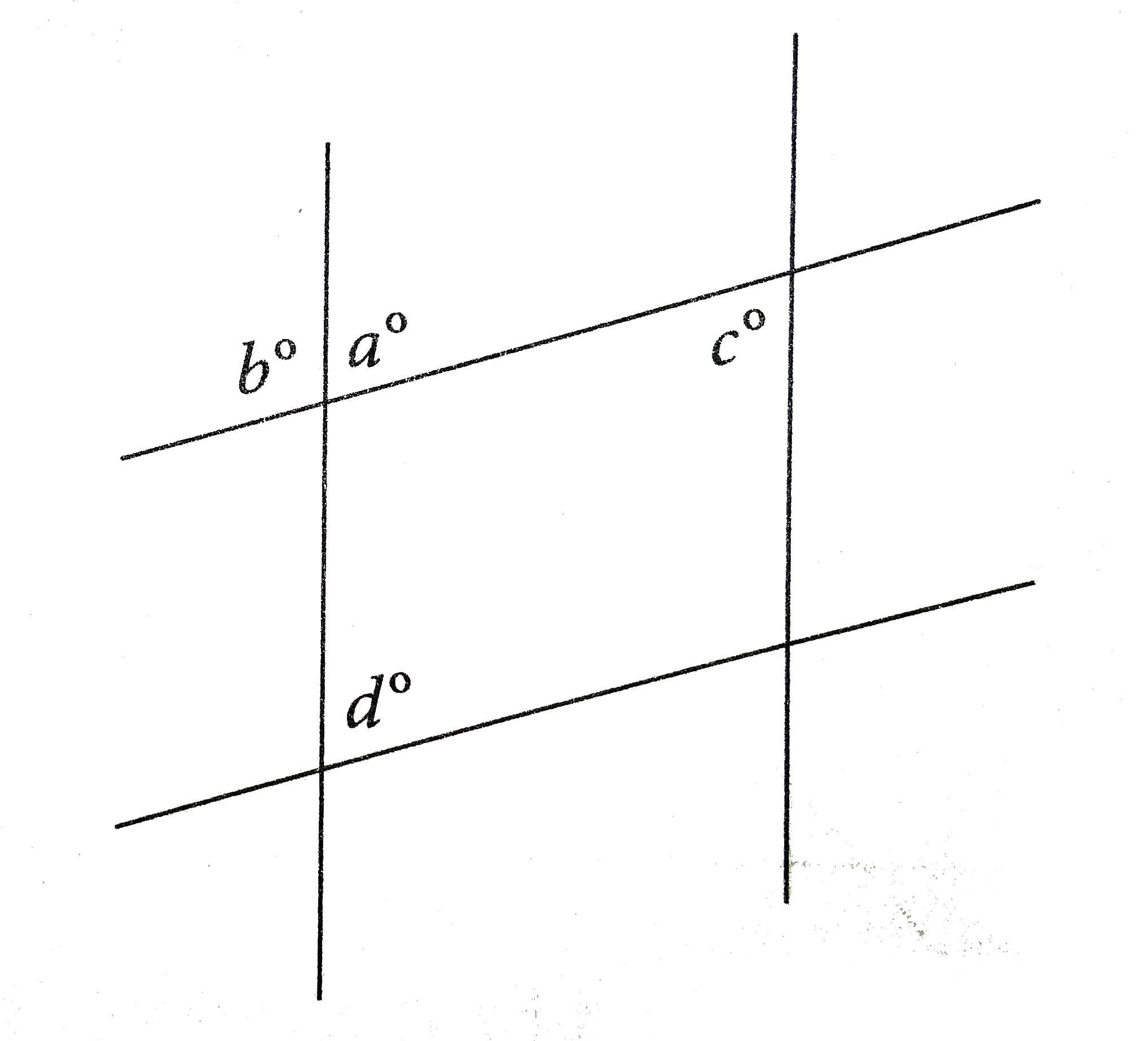
In Figure, which of the
following statements must be true?

(i) ${\displaystyle a+b=d+c}$

(ii) ${\displaystyle a+c+e={180}^0}$

(iii) ${\displaystyle b+f=c+e}$



(a) (i) only

(b) (ii) only

(c) (iii) only

(d) (ii) and (iii) only

Explanation

To solve the problem, we need to analyze each of the statements given in the question based on the relationships between the angles in the figure. Let's go through each statement step by step.

Step 1: Analyze Statement (i) \( a + b = d + c \)

1. Identify Relationships:
- Angles \( a \) and \( d \) are vertically opposite angles, which means \( a = d \).
- Angles \( b \) and \( e \) are also vertically opposite angles, which means \( b = e \).

2. Substitute Values:
- Since \( a = d \), we can rewrite \( a + b \) as \( d + e \).
- Therefore, \( a + b = d + e \) does not equal \( d + c \) unless \( e = c \), which is not necessarily true.

3. Conclusion:
- Statement (i) is false.

Step 2: Analyze Statement (ii) \( a + c + e = 180^\circ \)

1. Identify Relationships:
- We know that \( c \) and \( f \) are vertically opposite angles, so \( c = f \).

2. Rearrange the Equation:
- We can express \( a + c + e \) as \( a + f + e \) (since \( c = f \)).
- Angles \( a \) and \( e \) form a linear pair with angle \( f \), meaning \( a + f + e = 180^\circ \).

3. Conclusion:
- Statement (ii) is true.

Step 3: Analyze Statement (iii) \( b + f = c + e \)

1. Identify Relationships:
- From the previous analysis, we know \( b = e \) and \( c = f \).

2. Substitute Values:
- We can rewrite \( b + f \) as \( e + c \) (since \( b = e \)).
- Therefore, \( b + f = e + c \) is equivalent to \( c + e \).

3. Conclusion:
- Statement (iii) is true.

Final Conclusion

Based on the analysis of the statements:
- Statement (i) is false.
- Statement (ii) is true.
- Statement (iii) is true.

Thus, the correct answer is (d) (ii) and (iii) only.

---