Question

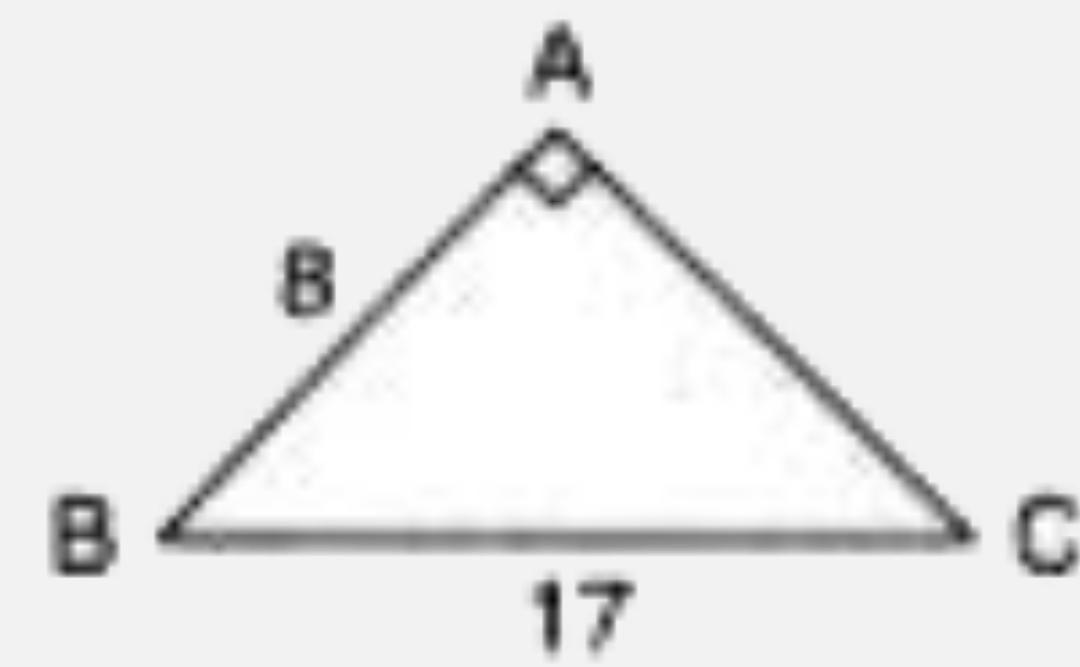
From Fig., write the values of: (i) $\tan B$
(ii) ${\sin }^{2}B+{\cos }^{2}B$

Explanation

To solve the question, we will find the values of $$\tan B$$ and $${\sin }^{2}B+{\cos }^{2}B$$ using the given information from the triangle BDC.

Step 1: Identify the sides of the triangle
From the problem, we have:
- \( CD = 4 \) (perpendicular)
- \( BD = 6 \) (base)

Step 2: Use the Pythagorean theorem to find the hypotenuse \( BC \)
According to the Pythagorean theorem:
\( BC^2 = CD^2 + BD^2 \)
Substituting the values:
\( BC^2 = 4^2 + 6^2 = 16 + 36 = 52 \)
Now, taking the square root to find \( BC \):
\( BC = \sqrt{52} = 2\sqrt{13} \)

Step 3: Calculate \( \tan B \)
The formula for \( \tan B \) is given by:
\( \tan B = \frac{\text{perpendicular}}{\text{base}} = \frac{CD}{BD} \)
Substituting the values:
\( \tan B = \frac{4}{6} = \frac{2}{3} \)

Step 4: Calculate \( \sin^2 B + \cos^2 B \)
Using the definitions of sine and cosine:
\( \sin B = \frac{\text{perpendicular}}{\text{hypotenuse}} = \frac{CD}{BC} = \frac{4}{2\sqrt{13}} = \frac{2}{\sqrt{13}} \)
\( \cos B = \frac{\text{base}}{\text{hypotenuse}} = \frac{BD}{BC} = \frac{6}{2\sqrt{13}} = \frac{3}{\sqrt{13}} \)

Now, we calculate \( \sin^2 B + \cos^2 B \):
\( \sin^2 B = \left(\frac{2}{\sqrt{13}}\right)^2 = \frac{4}{13} \)
\( \cos^2 B = \left(\frac{3}{\sqrt{13}}\right)^2 = \frac{9}{13} \)
Adding these together:
\( \sin^2 B + \cos^2 B = \frac{4}{13} + \frac{9}{13} = \frac{13}{13} = 1 \)

Final Answers:
(i) \( \tan B = \frac{2}{3} \)
(ii) \( \sin^2 B + \cos^2 B = 1 \)