What is the distance between two parallel tangents of a circle of radius 4 cm?
To find the distance between two parallel tangents of a circle with a radius of 4 cm, we can follow these steps:
1. Understand the Problem: We need to find the distance between two parallel tangents drawn to a circle with a given radius.
2. Identify the Radius: The radius of the circle is given as 4 cm.
3. Calculate the Diameter: The diameter of a circle is calculated using the formula:
Diameter=2×Radius
Substituting the given radius:
Diameter=2×4 cm=8 cm
4. Distance Between Parallel Tangents: According to the properties of tangents to a circle, the distance between two parallel tangents is equal to the diameter of the circle. Therefore, the distance between the two parallel tangents is:
Distance=Diameter=8 cm
5. Final Answer: The distance between the two parallel tangents of the circle is 8 cm.
Diameter=2×Radius
Substituting the given radius:
Diameter=2×4 cm=8 cm
Distance=Diameter=8 cm
Topper's Solved these Questions
Similar Questions
Knowledge Check
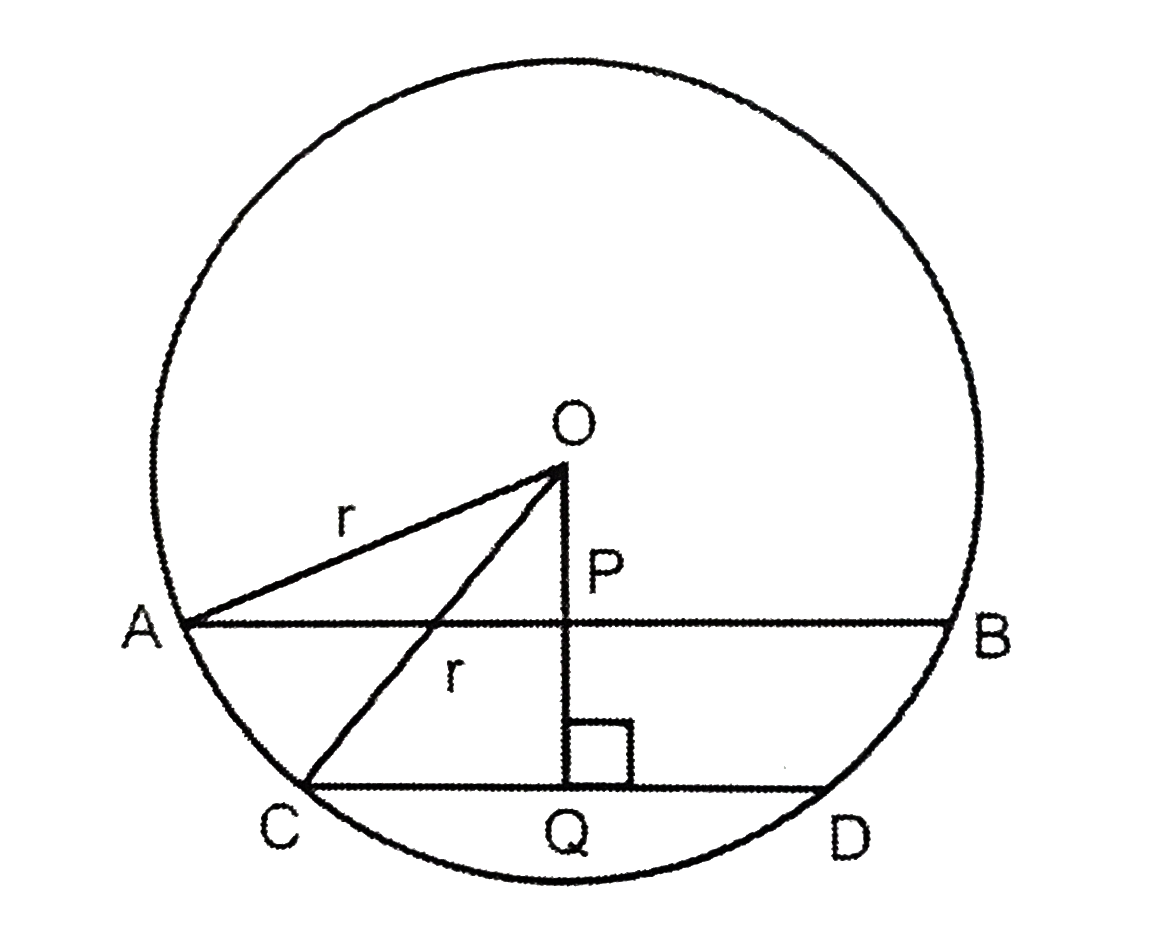
2 parallel chords 24 cm, and 18 cm, are on the same side of the centre of a circle. If the distance between the chords is 3 cm, calculate the radius of the circle.A15 cmB14 cmC13 cmD12 cm
Assertion (A): The polar of centre of circle w.r.t same circle does not exist.
Reason (R), Distance between parallel tangents of circle is diameter of circle.
The correct answer is
View SolutionIf the distance between the centres of two circles of radio 3,4 is 25 then the length of the tranverse common tangent is
View SolutionEach side of a rhombus is 18 cm. If the distance between two parallel sides is 12 cm, find its area.
View SolutionFrom a point P which is at a distance of 13 cm from the center O of a circle of radius 5 cm, the pair of tangents PQ and PR to the circle is drawn. Then, the area of the quadrilateral PQOR is
View SolutionFind the length of a chord which is at a distance of 4 cm from the centre of the circle of radius 6 cm.
View SolutionDraw a circle of radius 4 cm. Construct a pair of tangents to it, the angle between which is 60∘. Also justify the construction. Measure the distance between the centre of the circle and the point of intersection of tangents.
View SolutionLet PQ and RS be two parallel chords of a given circle of radius 6 cm, lying on the same side of the center. If the chords subtends angles of 72∘and 144∘ at the center and the distance between the chords is d, then d2 is equal to
View Solution
