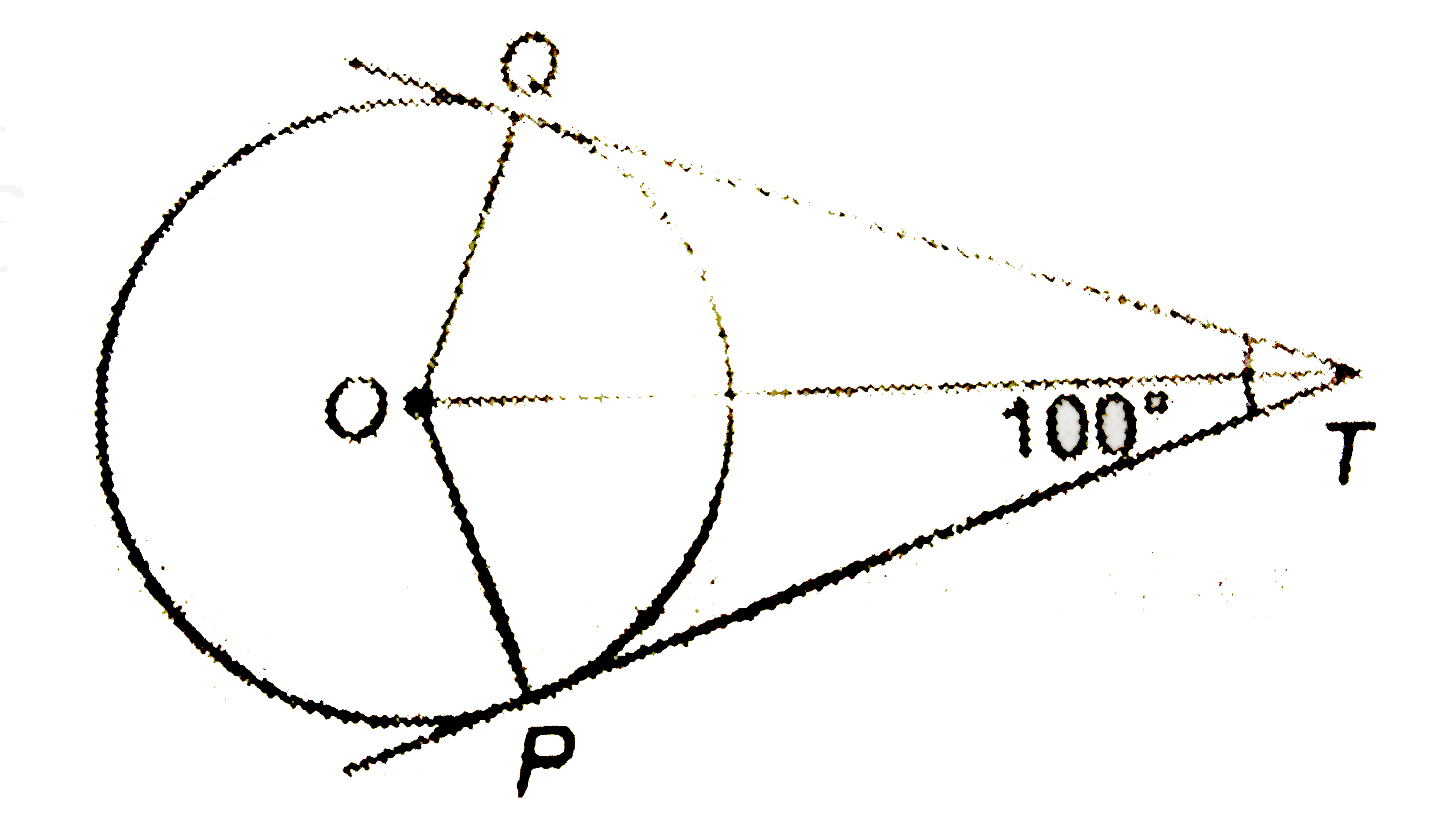
Two tangents TP and TQ are drawn from an external point T to a circle with centre O as shown in Fig. 10.73. If they are inclined to each other at an angle of 100o , then what is the value of ∠POQ ?
To solve the problem, we need to find the angle ∠POQ given that the tangents TP and TQ from the external point T to the circle with center O are inclined to each other at an angle of 100∘.
1. Understanding the Geometry:
- When two tangents are drawn from an external point to a circle, they form two angles with the line joining the external point to the center of the circle.
- The angles formed between the tangents and the line joining the external point to the center of the circle are equal.
2. Label the Angles:
- Let ∠OTP be the angle between the tangent TP and the line OT.
- Let ∠OTQ be the angle between the tangent TQ and the line OT.
- Since TP and TQ are tangents from point T, we have ∠OTP=∠OTQ.
3. Using the Given Information:
- We know that the angle between the two tangents TP and TQ is given as 100∘.
- Therefore, we can express this relationship as:
∠PTQ=∠OTP+∠OTQ=2∠OTP=100∘
4. Finding ∠OTP:
- From the equation 2∠OTP=100∘, we can solve for ∠OTP:
∠OTP=100∘2=50∘
5. Finding ∠POQ:
- The angle ∠POQ is the angle at the center of the circle subtended by the points P and Q.
- According to the property of tangents, the angle at the center is twice the angle at the circumference. Therefore:
∠POQ=2×∠OTP=2×50∘=100∘
Final Answer:
∠POQ=100∘
- When two tangents are drawn from an external point to a circle, they form two angles with the line joining the external point to the center of the circle.
- The angles formed between the tangents and the line joining the external point to the center of the circle are equal.
- Let ∠OTP be the angle between the tangent TP and the line OT.
- Let ∠OTQ be the angle between the tangent TQ and the line OT.
- Since TP and TQ are tangents from point T, we have ∠OTP=∠OTQ.
- We know that the angle between the two tangents TP and TQ is given as 100∘.
- Therefore, we can express this relationship as:
∠PTQ=∠OTP+∠OTQ=2∠OTP=100∘
- From the equation 2∠OTP=100∘, we can solve for ∠OTP:
∠OTP=100∘2=50∘
- The angle ∠POQ is the angle at the center of the circle subtended by the points P and Q.
- According to the property of tangents, the angle at the center is twice the angle at the circumference. Therefore:
∠POQ=2×∠OTP=2×50∘=100∘
∠POQ=100∘
Topper's Solved these Questions
Similar Questions
Two tangents TP and TQ are drawn from an external point T to a circle with centre O as shown in figure. If they are inclined to each other at an angle of 100∘, then what is the value of ∠POQ?
View SolutionTwo tangents PQ and PR are drawn from an external point to a circle with centre O. Prove that QORP is cyclic quadrilateral.
View SolutionTwo tangents PAandPB are drawn from an external point P to a circle with centre O. Prove that AOBP is a cyclic quadrilateral.
View Solutiontwo tangents RQ and RP are drawn from an external point R to the circle with centre O. If ∠PRQ=120∘ , then prove that OR= PR+ RQ
View SolutionTwo tangents TP and TQ are drawn to a circle with centre O from an external point T . Prove that ∠PTQ=2∠OPQ .
View SolutionTwo tangents TP and TQ are drawn to a circle with centre O from an external point T . Prove that ∠PTQ=2∠OPQ .
View SolutionPA and PB are two tangents drawn from an external point P to a circle with centre C and radius=4cm If PA⊥PB then length of each tangent is
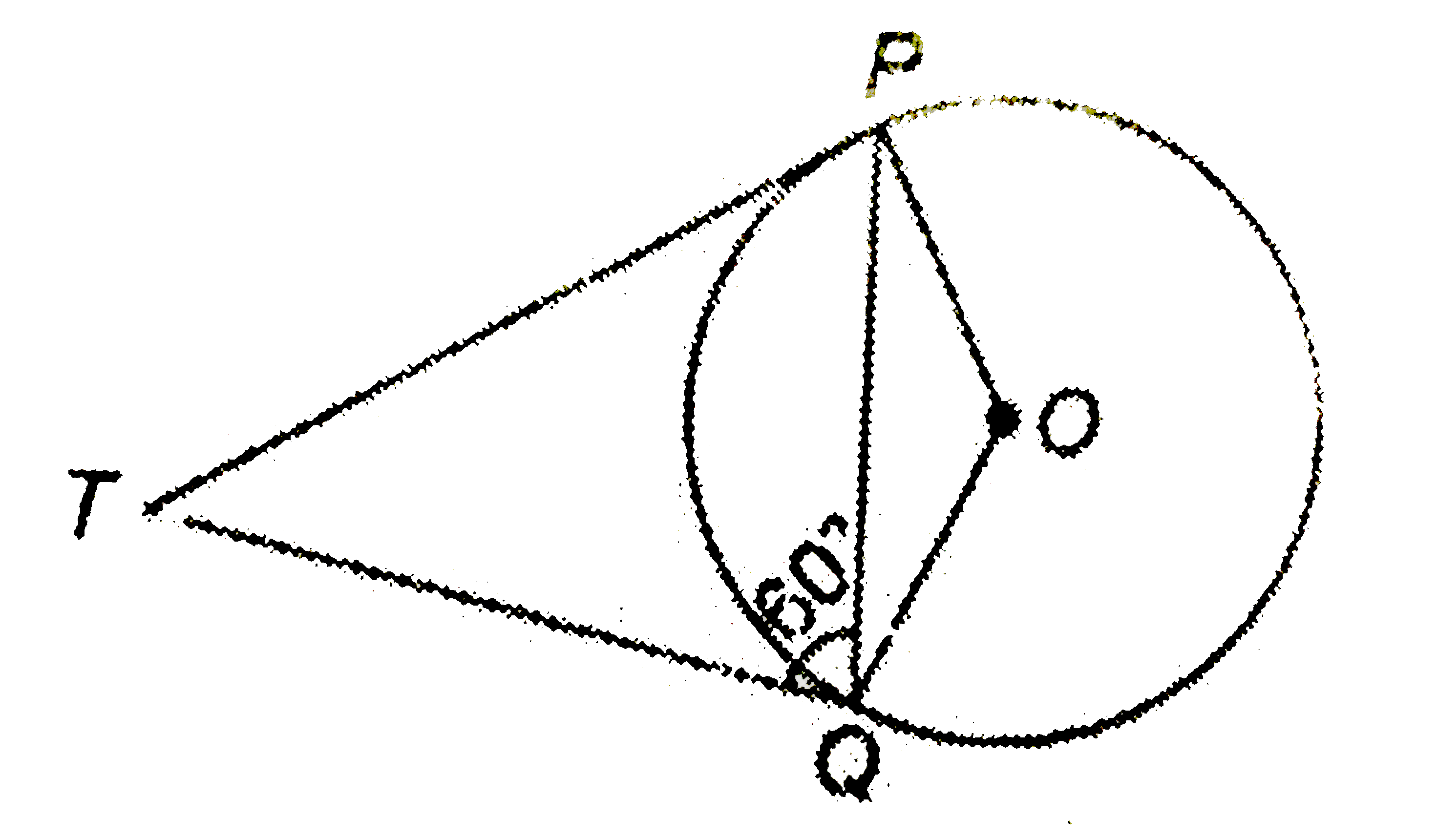
View SolutionIn the given figure, TP and TQ are tangents drawn from an external point T to a circle with centre O such that ∠TQP=60∘. Find angelOPQ.
View SolutionIf tangents PA and PB from a point P to a circle with centre O are inclined to each other at an angle of 80o then ∠POA is equal to :
View SolutionIf tangents PA and PB from a point P to a circle with centre O are inclined to each other at angle of 80∘, then ∠POA is equal to
View Solution