The area enclosed between the concentric circles is 770 cm2 . If the radius of the outer circle is 21 cm, find the radius of the inner circle.
To find the radius of the inner circle given the area enclosed between two concentric circles and the radius of the outer circle, we can follow these steps:
1. Identify the Given Values:
- Area enclosed between the concentric circles = 770 cm²
- Radius of the outer circle (R) = 21 cm
2. Formula for the Area of a Circle:
The area of a circle is given by the formula:
Area=πr2
where r is the radius of the circle.
3. Set Up the Equation:
The area enclosed between the two circles can be expressed as:
Area of outer circle−Area of inner circle=Area enclosed
This can be written as:
πR2−πr2=770
where r is the radius of the inner circle.
4. Factor Out π:
We can factor out π from the left side:
π(R2−r2)=770
5. Substitute the Value of R:
Substitute R=21 cm into the equation:
π(212−r2)=770
6. Calculate 212:
Calculate 212:
212=441
So the equation becomes:
π(441−r2)=770
7. Substitute π Value:
Using π≈227:
227(441−r2)=770
8. Cross Multiply to Eliminate the Fraction:
Cross-multiply to simplify:
22(441−r2)=770×7
9. Calculate 770×7:
Calculate the right side:
770×7=5390
So the equation becomes:
22(441−r2)=5390
10. Divide Both Sides by 22:
Divide both sides by 22:
441−r2=539022
11. Calculate 539022:
Calculate:
539022=245
So now we have:
441−r2=245
12. Rearrange to Find r2:
Rearranging gives:
r2=441−245
13. Calculate 441−245:
Calculate:
441−245=196
Thus:
r2=196
14. Take the Square Root:
Taking the square root of both sides gives:
r=√196=14
15. Conclusion:
Therefore, the radius of the inner circle is:
r=14 cm
Final Answer:
The radius of the inner circle is 14 cm.
- Area enclosed between the concentric circles = 770 cm²
- Radius of the outer circle (R) = 21 cm
The area of a circle is given by the formula:
Area=πr2
where r is the radius of the circle.
The area enclosed between the two circles can be expressed as:
Area of outer circle−Area of inner circle=Area enclosed
This can be written as:
πR2−πr2=770
where r is the radius of the inner circle.
We can factor out π from the left side:
π(R2−r2)=770
Substitute R=21 cm into the equation:
π(212−r2)=770
Calculate 212:
212=441
So the equation becomes:
π(441−r2)=770
Using π≈227:
227(441−r2)=770
Cross-multiply to simplify:
22(441−r2)=770×7
Calculate the right side:
770×7=5390
So the equation becomes:
22(441−r2)=5390
Divide both sides by 22:
441−r2=539022
Calculate:
539022=245
So now we have:
441−r2=245
Rearranging gives:
r2=441−245
Calculate:
441−245=196
Thus:
r2=196
Taking the square root of both sides gives:
r=√196=14
Therefore, the radius of the inner circle is:
r=14 cm
The radius of the inner circle is 14 cm.
Topper's Solved these Questions
Similar Questions
The area of a circle is 616 cm2. Find the radius of the circle.
View SolutionThe area of a circle is 154 cm2. Find the radius of the circle.
View SolutionThe area enclosed by the circumference of two concentric circles is 423.5cm2. If the circumference of outer circle is 132 cm. Calculate the radius of the inner circle
View SolutionThe diameter of a circle is 9 cm, find its radius.
View SolutionTwo circles have an external tangent with length 36 cm. The shortest distance between these circles is 14 cm. If the radius of the longer circle is 4 times the radius of the smaller circle then the radius of the larger circle in cms is
View SolutionThe area of a circular ring enclosed between two concentric circles is 286 cm? Find the radii of the two circles, given that their difference is 7 cm.
View SolutionIn the figure, when the outer circles all have radii 'r', then the radius of the inner circle will be
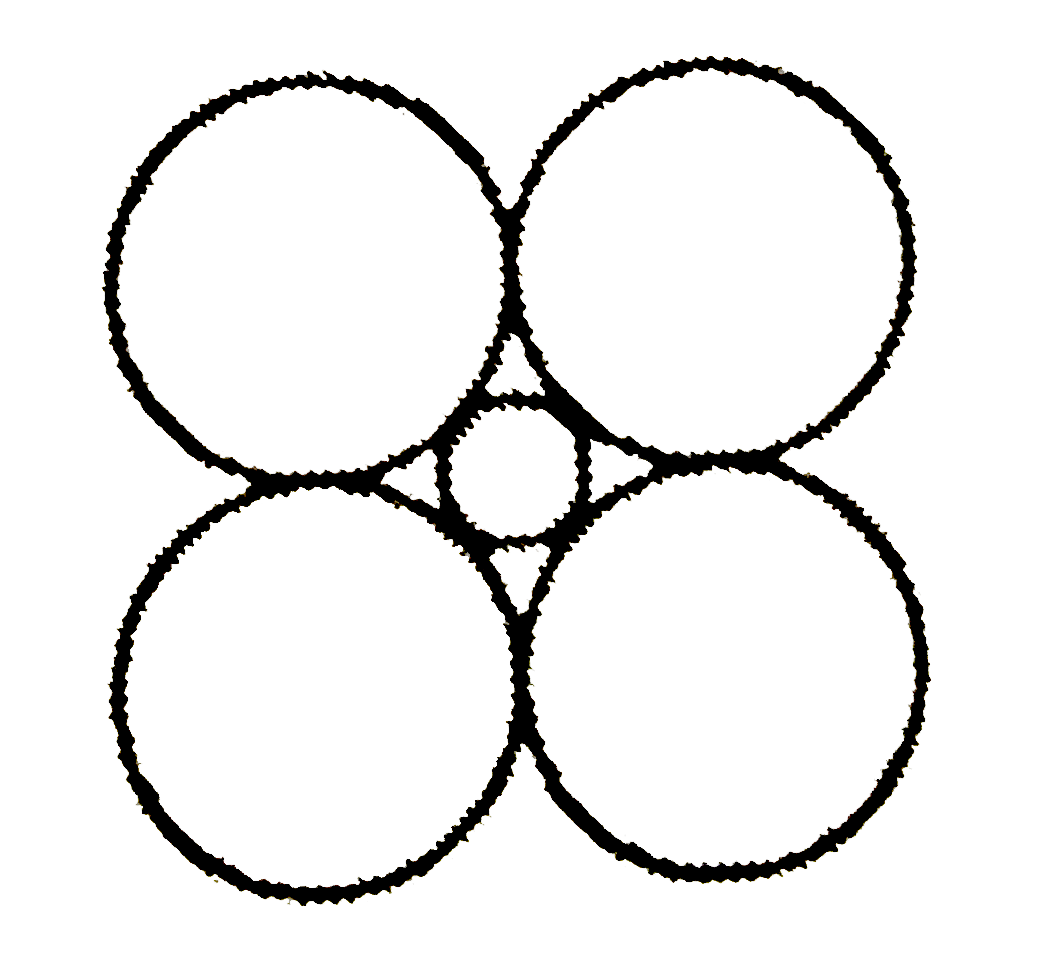
View SolutionThe difference between the circumference and radius of a circle is 37 cm. Find the area of the circle
View SolutionThe radius of a circle is 14 cm. Find the radius of the circle whose area is double of the area of the circle.
View SolutionIf the radius of a circle is 3 times that of another circle, find the ratio of their areas.
View Solution
