To warn ships for underwater rocks, a light house throws a red coloured light over a sector of 80o angle to a distance of 16.5 km. Find the area of the sea over which the ships are warned.
To find the area of the sea over which the ships are warned by the lighthouse, we can follow these steps:
Step 1: Understand the Problem
The lighthouse throws light over a sector of 80∘ with a radius of 16.5 km. We need to find the area of this sector.
Step 2: Recall the Formula for the Area of a Sector
The formula for the area A of a sector of a circle is given by:
A=θ360∘×πr2
where:
- A is the area of the sector,
- θ is the angle of the sector in degrees,
- r is the radius of the circle.
Step 3: Substitute the Known Values
Here, θ=80∘ and r=16.5 km. Plugging these values into the formula gives:
A=80360×π×(16.5)2
Step 4: Calculate (16.5)2
First, calculate (16.5)2:
(16.5)2=272.25
Step 5: Substitute and Simplify
Now substitute (16.5)2 back into the area formula:
A=80360×π×272.25
Next, simplify 80360:
80360=29
Now substitute this back into the equation:
A=29×π×272.25
Step 6: Use π≈227
To calculate the area, we can use π≈227:
A=29×227×272.25
Step 7: Calculate the Area
Now, calculate the area:
1. First, calculate 2×22×272.259×7:
=44×272.2563
2. Calculate 44×272.25=11979.
3. Now divide by 63:
A≈1197963≈189.97 km2
Conclusion
The area of the sea over which the ships are warned is approximately 189.97 km2.
---
The lighthouse throws light over a sector of 80∘ with a radius of 16.5 km. We need to find the area of this sector.
The formula for the area A of a sector of a circle is given by:
A=θ360∘×πr2
where:
- A is the area of the sector,
- θ is the angle of the sector in degrees,
- r is the radius of the circle.
Here, θ=80∘ and r=16.5 km. Plugging these values into the formula gives:
A=80360×π×(16.5)2
First, calculate (16.5)2:
(16.5)2=272.25
Now substitute (16.5)2 back into the area formula:
A=80360×π×272.25
Next, simplify 80360:
80360=29
Now substitute this back into the equation:
A=29×π×272.25
To calculate the area, we can use π≈227:
A=29×227×272.25
Now, calculate the area:
1. First, calculate 2×22×272.259×7:
=44×272.2563
2. Calculate 44×272.25=11979.
3. Now divide by 63:
A≈1197963≈189.97 km2
The area of the sea over which the ships are warned is approximately 189.97 km2.
Topper's Solved these Questions
Similar Questions
To warn ships for underwater rocks, a lighthouse spreads a red coloured light over a sector of angle 80∘to a distance of 16.5 km. Find the area of the sea over which the ships are warned.
View SolutionTo warn ships for underwater rocks, a lighthouse spreads a red coloured light over a sector of angle 80oto a distance of 16.5 km. Find the area of the sea over which the ships are warned.
View SolutionA ring of mass m=1kg can slide over a smooth vertical rod. A light string attached to the ring passing over a smooth fixed pulley at a distance of L=0.7m from the rod as shown in figure.
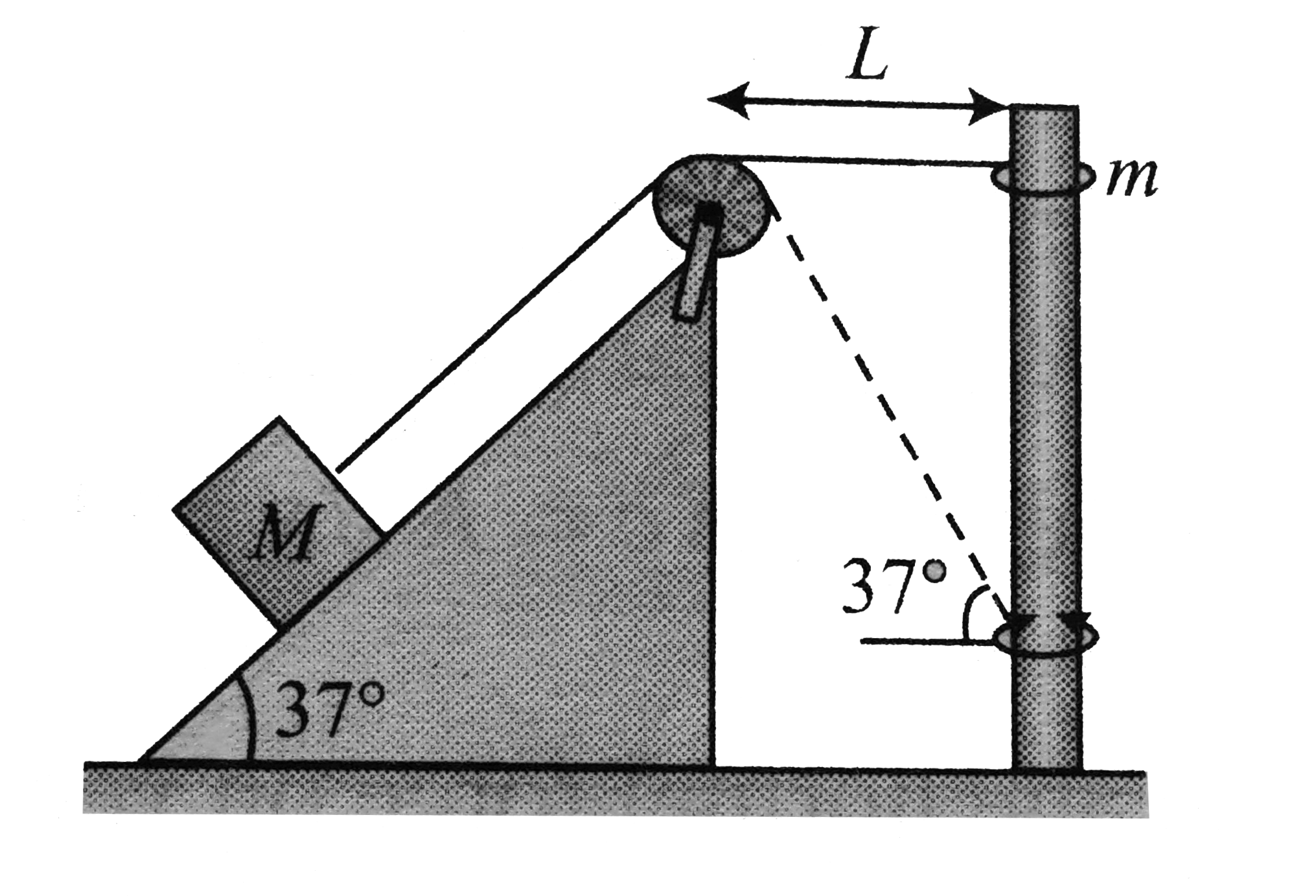
At the other end of the string mass M=5kg is attached, lying over a smooth fixed inclined plane of inclination angle 37∘. The ring is held in level with the pulley and released. Determine the velocity of ring when the string makes an angle (α=37∘) with the horizontal. [sin37∘=0.6]
View SolutionTwo ships are there in the sea on either side of a light house in such a way that the ships and the light house are in the same straight line. The angles of depression of two ships are observed from the top of the light house are 60∘ and 45∘ respectively. If the height of the light house is 200 m, find the distance between the two ships. (Use √3=1.73)
View SolutionForm the top of a light house 60 m high with its base at the sea-level the angle of depression of a boat is 15∘. Find the distance of the boat from the foot of light house.
View SolutionA driver having a definite reaction time is capable of stopping his car over a distance of 30 m on seeing a red traffic signal, when the speed of the car is 72 km/hr andover a distance of 10 m when the speed is 36 km/hr. Find the distance over which he can stop the car if it were running at a speed of 54 km/hr. Assume that his reaction time and the deceleration of the car remains same in all the three cases.
View SolutionIn Yonung's double-slit experiment, two slits which are separated by 1.2 mm are illuminated with a monochromatic light of wavelength 6000Å The interference pattern is observed on a screen placed at a distance of 1 m from the slits. Find the number of bright fringes formed over 1 cm width on the screen.
View SolutionThe height of a light house is 40 m. The angle of depression of a ship from the top of the light house is 60∘. Find the distance of ship from the light house.
View SolutionThe angles of depression of two ships from the top of a light house and on the same side of it are found to be 45∘ and 30∘ respectively. If the ships are 200m apart, find the height of the light house.
View SolutionThe angles of depression of two ships a A and B as observed from the top of a light house 60 m high are 60∘and45∘ respectively. If the two ships are on the opposite sides of the light house, find the distance between the two ships. Give your answer correct to the nearest whole number.
View Solution
