AB is a chord of a circle with centre O and radius 4 cm. AB is of length 4 cm. Find the area of sector of the circle formed by chord AB .
To find the area of the sector of the circle formed by the chord AB, we can follow these steps:
Step 1: Understand the Given Information
We have a circle with:
- Center O
- Radius r=4 cm
- Chord AB=4 cm
Step 2: Draw the Diagram
Draw a circle with center O. Mark points A and B on the circumference such that AB is a chord of length 4 cm.
Step 3: Identify the Triangle
Connect points O to A and O to B. This forms triangle OAB. Since OA and OB are both radii of the circle, we have:
- OA=OB=4 cm
- AB=4 cm
Step 4: Determine the Type of Triangle
Since all sides of triangle OAB are equal (4 cm), triangle OAB is an equilateral triangle. Therefore, each angle in triangle OAB is 60∘.
Step 5: Use the Area of Sector Formula
The area A of a sector of a circle is given by the formula:
A=θ360∘×πr2
where θ is the angle in degrees and r is the radius.
Step 6: Substitute the Values
Here, θ=60∘ and r=4 cm. Substitute these values into the formula:
A=60360×π×(4)2
Step 7: Simplify the Expression
First, simplify 60360:
60360=16
Now, calculate (4)2=16:
A=16×π×16
A=16π6
Now simplify 16π6:
A=8π3 cm2
Step 8: Substitute π for Approximation (Optional)
If you want a numerical approximation, use π≈227:
A≈8×2273=17621 cm2
Final Answer
The area of the sector formed by chord AB is:
8π3 cm2or approximately 17621 cm2
---
We have a circle with:
- Center O
- Radius r=4 cm
- Chord AB=4 cm
Draw a circle with center O. Mark points A and B on the circumference such that AB is a chord of length 4 cm.
Connect points O to A and O to B. This forms triangle OAB. Since OA and OB are both radii of the circle, we have:
- OA=OB=4 cm
- AB=4 cm
Since all sides of triangle OAB are equal (4 cm), triangle OAB is an equilateral triangle. Therefore, each angle in triangle OAB is 60∘.
The area A of a sector of a circle is given by the formula:
A=θ360∘×πr2
where θ is the angle in degrees and r is the radius.
Here, θ=60∘ and r=4 cm. Substitute these values into the formula:
A=60360×π×(4)2
First, simplify 60360:
60360=16
Now, calculate (4)2=16:
A=16×π×16
A=16π6
Now simplify 16π6:
A=8π3 cm2
If you want a numerical approximation, use π≈227:
A≈8×2273=17621 cm2
The area of the sector formed by chord AB is:
8π3 cm2or approximately 17621 cm2
Topper's Solved these Questions
Similar Questions
Construct a circle with centre O and radius 4 cm.
View SolutionIn a circle with centre O and radius 5cm, AB is a chord of length 5√3cm . Find the area of sector AOB.
View SolutionAB is a chord of a circle with centre O and radius 4 cm. AB is of length 4 cm and divides the circle into two segments. Find the area of the minor segment.
View SolutionGiven a circle with centre O and radius 2.5 cm, what is the length of the longest chord of the circle
View SolutionA chord of a circle of diameter 30 cm is of length 15 cm. Find the length of mirror arc corresponding to this chord.
View SolutionA chord of a circle of radius 14 cm makes a right angle at the centre. Find the areas of the minor and major segments of the circle.
View SolutionA chord of a circle of radius 12 cm subtends an angle of 120∘at the centre. Find the area of the corresponding segment of the circle.
View SolutionA chord AB of a circle, of radius 14 cm makes an angle of 60∘ at the centre of the circle. Find the area of the minor segment of the circle.
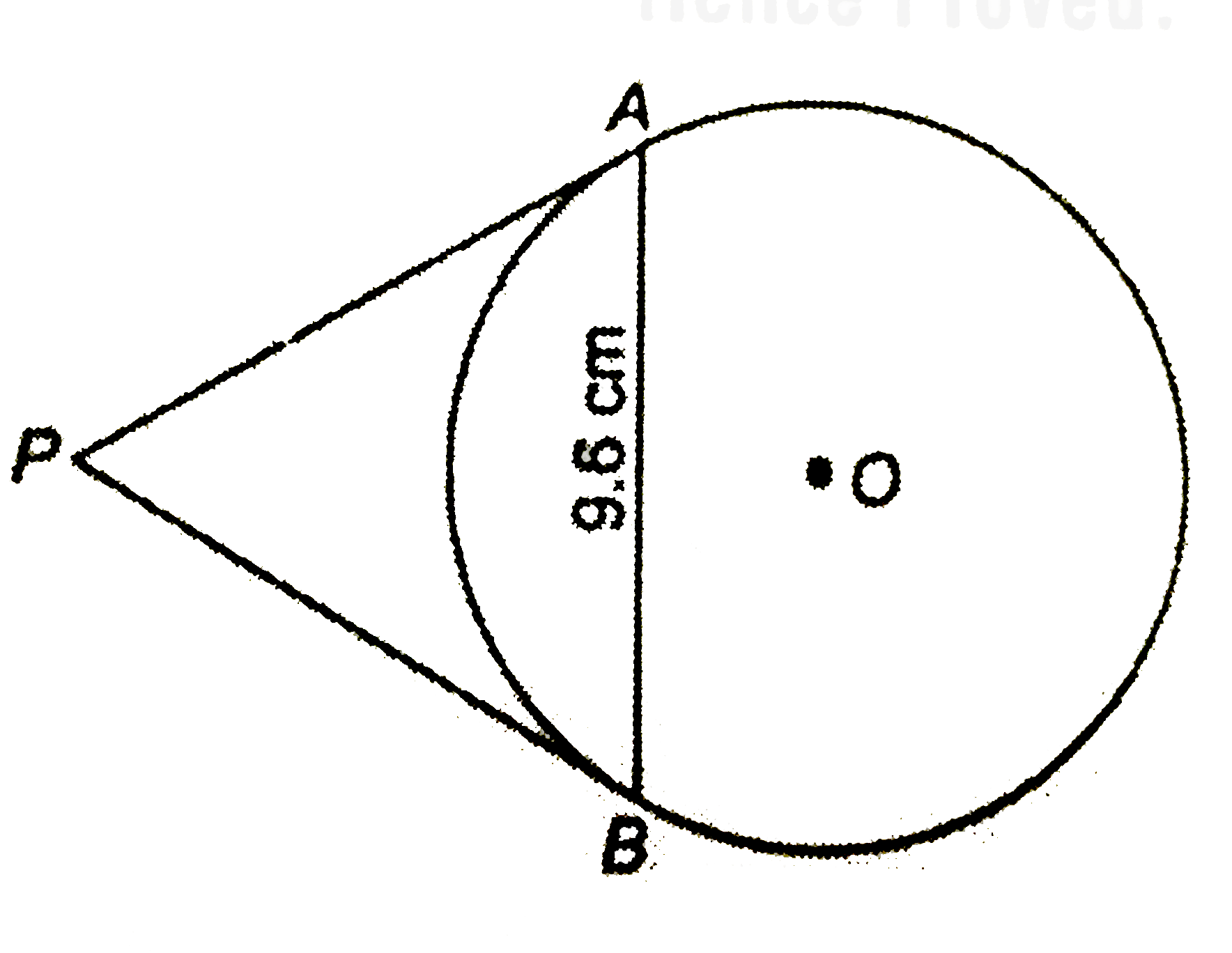
View SolutionIn the adjoining figure, AB is a chord of length 9.6 cm of a circle with centre O and radius 6 cm. The tangents at A and B intersect at P. Find the length of PA.
View SolutionThe perimeter of a sector of a circle of radius 5.2cm is 16.4cm. Find the area of the sector.
View Solution