In a circle with centre O and radius 5cm, AB is a chord of length 5√3cm . Find the area of sector AOB.
To find the area of sector AOB in a circle with center O and radius 5 cm, where AB is a chord of length 5√3 cm, we can follow these steps:
Step 1: Identify the given values
- Radius of the circle (OA or OB) = 5 cm
- Length of chord AB = 5√3 cm
Step 2: Find the length of AM
Since M is the midpoint of chord AB, we can find the length of AM:
AM=AB2=5√32 cm
Step 3: Use the right triangle AOM
In triangle AOM, we can use the sine function to find the angle θ:
sin(θ)=AMOA
Substituting the values:
sin(θ)=5√325=√32
Step 4: Determine the angle θ
From the sine value, we know:
sin(θ)=√32⟹θ=60∘
Step 5: Find angle AOB
Since angle AOB is twice angle AOM:
∠AOB=2×θ=2×60∘=120∘
Step 6: Calculate the area of sector AOB
The formula for the area of a sector is given by:
Area of sector=θ360∘×πr2
Substituting the values:
Area of sector=120360×π×(5)2
=13×π×25=25π3 cm2
Final Answer
Thus, the area of sector AOB is:
25π3 cm2
- Radius of the circle (OA or OB) = 5 cm
- Length of chord AB = 5√3 cm
Since M is the midpoint of chord AB, we can find the length of AM:
AM=AB2=5√32 cm
In triangle AOM, we can use the sine function to find the angle θ:
sin(θ)=AMOA
Substituting the values:
sin(θ)=5√325=√32
From the sine value, we know:
sin(θ)=√32⟹θ=60∘
Since angle AOB is twice angle AOM:
∠AOB=2×θ=2×60∘=120∘
The formula for the area of a sector is given by:
Area of sector=θ360∘×πr2
Substituting the values:
Area of sector=120360×π×(5)2
=13×π×25=25π3 cm2
Thus, the area of sector AOB is:
25π3 cm2
Topper's Solved these Questions
Similar Questions
AB is a chord of a circle with centre O and radius 4 cm. AB is of length 4 cm. Find the area of sector of the circle formed by chord AB .
View SolutionDraw a circle with centre O and radius 5 cm. draw a chord CD of length less than the diameter of the circle.
Draw the perpendicular bisector of CD. Does it pass from point O ?
View SolutionGiven a circle with centre O and radius 2.5 cm, what is the length of the longest chord of the circle
View SolutionAB is a chord of a circle with centre O and radius 4 cm. AB is of length 4 cm and divides the circle into two segments. Find the area of the minor segment.
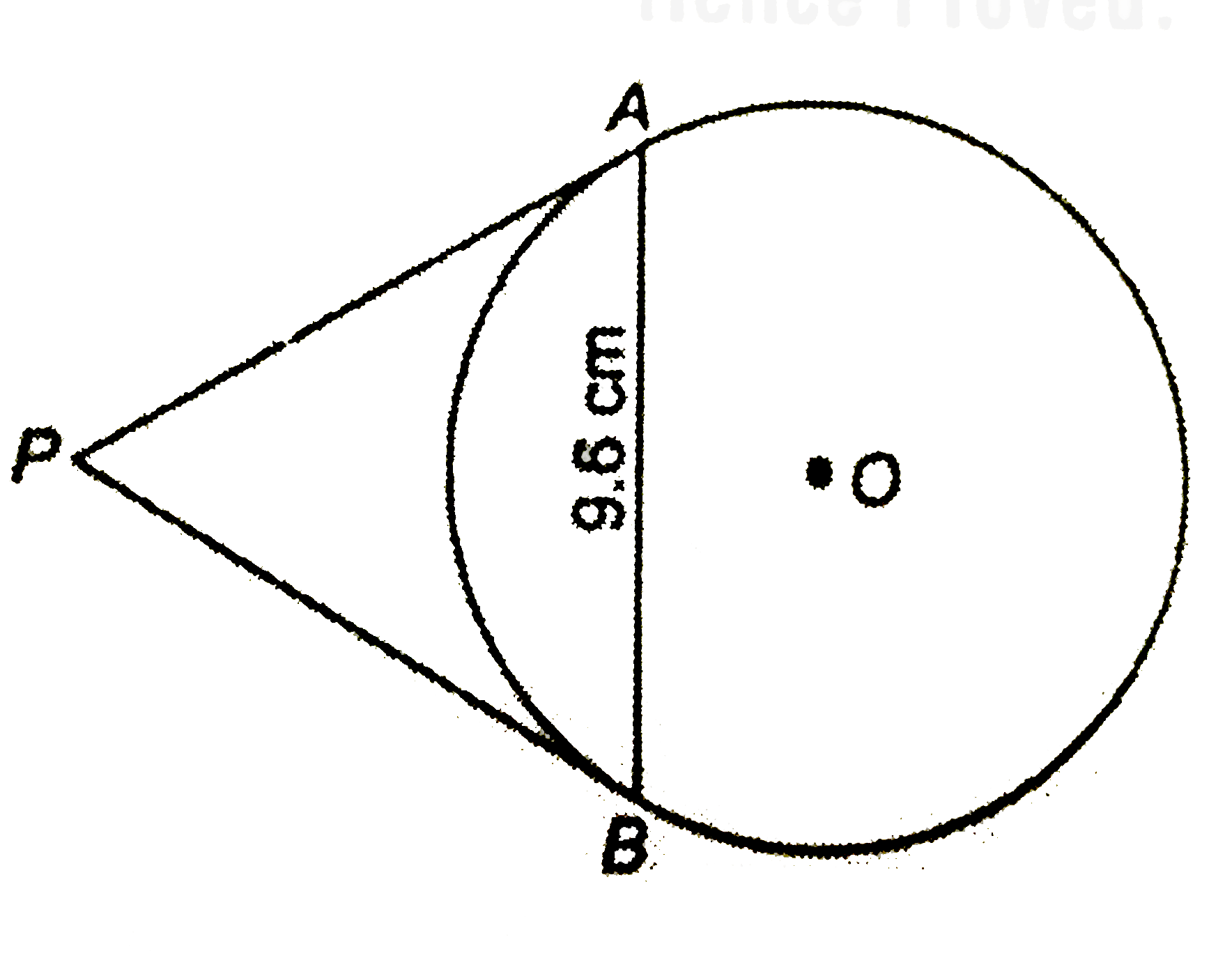
View SolutionIn the adjoining figure, AB is a chord of length 9.6 cm of a circle with centre O and radius 6 cm. The tangents at A and B intersect at P. Find the length of PA.
View SolutionIn Figure, OACB is a quadrant of a circle with centre O and radius 3.5 cm. If OD=2 cm , find the area of the (i) quadrant OACB (ii) shaded region.
View SolutionDraw a circle with centre at point O and radius 5cm. Draw its chord AB, draw the perpendicular bisector of line segment AB. Does it pass through the centre of the circle?
View SolutionIn Fig. 12.30, OACB is a quadrant of a circle with centre O and radius 3.5 cm. If OD=2cm, find the area of the
(i) quadrant OACB,
(ii) shaded region.
View SolutionDraw a circle with centre at a point O and radius 5.6 cm. Draw any chord AB. Draw a perpendicular bisector of AB. Does the bisector pass through the centre O ?
View SolutionA sector of a circle of radius 8 cm contains an angle of 135o . Find the area of the sector.
View Solution
