Determine the measure of each of the equal angles of a right-angled isosceles triangle.
To determine the measure of each of the equal angles of a right-angled isosceles triangle, we can follow these steps:
1. Understand the Properties of a Right-Angled Isosceles Triangle:
- A right-angled isosceles triangle has one angle that measures 90 degrees. The other two angles are equal.
2. Identify the Angles:
- Let’s denote the triangle as ABC, where angle B is the right angle (90 degrees). Therefore, angle B = 90°.
3. Use the Triangle Sum Property:
- The sum of all angles in a triangle is always 180 degrees. Thus, we can write the equation:
Angle A+Angle B+Angle C=180°
- Since angle B = 90°, we can substitute this into the equation:
Angle A+90°+Angle C=180°
4. Recognize the Isosceles Property:
- In an isosceles triangle, the angles opposite the equal sides are equal. Therefore, angle A = angle C.
5. Substitute and Simplify:
- Since angle A = angle C, we can denote both angles as x:
x+90°+x=180°
- This simplifies to:
2x+90°=180°
6. Isolate x:
- To isolate x, subtract 90° from both sides:
2x=180°−90°
2x=90°
7. Solve for x:
- Divide both sides by 2:
x=90°2=45°
8. Conclusion:
- Therefore, each of the equal angles (angle A and angle C) measures 45 degrees.
Final Answer:
Each of the equal angles of the right-angled isosceles triangle measures 45 degrees.
---
- A right-angled isosceles triangle has one angle that measures 90 degrees. The other two angles are equal.
- Let’s denote the triangle as ABC, where angle B is the right angle (90 degrees). Therefore, angle B = 90°.
- The sum of all angles in a triangle is always 180 degrees. Thus, we can write the equation:
Angle A+Angle B+Angle C=180°
- Since angle B = 90°, we can substitute this into the equation:
Angle A+90°+Angle C=180°
- In an isosceles triangle, the angles opposite the equal sides are equal. Therefore, angle A = angle C.
- Since angle A = angle C, we can denote both angles as x:
x+90°+x=180°
- This simplifies to:
2x+90°=180°
- To isolate x, subtract 90° from both sides:
2x=180°−90°
2x=90°
- Divide both sides by 2:
x=90°2=45°
- Therefore, each of the equal angles (angle A and angle C) measures 45 degrees.
Each of the equal angles of the right-angled isosceles triangle measures 45 degrees.
Topper's Solved these Questions
Similar Questions
Find the measures of each of the two equal angles of an isosceles right-angled triangle.
View SolutionIn a ΔPQR, if ∠P=90∘ and ∠Q=∠R, find the measures of each of the equal angles of the triangle.
View SolutionThe acute angle between the medians drawn from the acute angles of a right angle isosceles triangle is
View SolutionThe distance between the two lines represented by the sides of an equilateral triangle a right-angled triangle an isosceles triangle
View SolutionFind the measure of each angle of an equilateral triangle.
View SolutionFind the measure of each exterior angle of an equilateral triangle.
View SolutionThree charges Q, +q and +q are placed at the vertices of a right-angled isosceles triangle as shown. The net electrostatic energy of the configuration is zero if Q is equal to
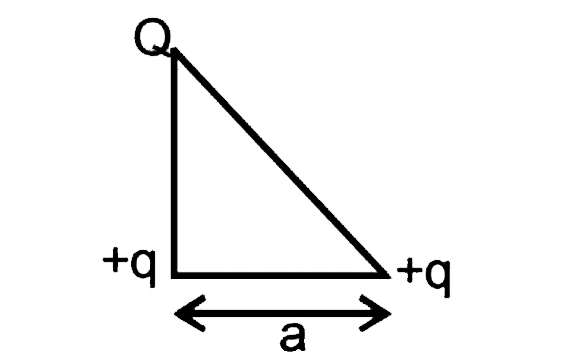
View SolutionThree charges Q, +q and +q are placed at the vertices of a right-angled isosceles triangle as shown. The net electrostatic energy of the configuration is zero if Q is equal to

View SolutionIf a vertex, the circumcenter, and the centroid of a triangle are (0, 0), (3,4), and (6, 8), respectively, then the triangle must be (a) a right-angled triangle (b) an equilateral triangle (c) an isosceles triangle (d) a right-angled isosceles triangle
View SolutionIf one angle of a triangle is equal to the sum of the other two angles, then the triangle is (a) an isosceles triangle (b) an obtuse triangle (c) an equilateral triangle (d) a right triangle
View Solution
