In Figure, PQR is a triangle and S is any point in its interior, show that SQ+SR<PQ+PR. Given : S is any point in the interior of PQR To Prove : SQ+SR<PQ+PR Construction: Produce QS to meet PR in T
To prove that SQ+SR<PQ+PR for triangle PQR with point S in its interior, we can follow these steps:
Step 1: Construct the triangle and extend line QS
- Draw triangle PQR with point S inside it.
- Extend line QS to meet line PR at point T.
Hint: Visualizing the triangle and the point can help in understanding the relationships between the segments.
Step 2: Apply the Triangle Inequality in triangle PQT
- In triangle PQT, by the triangle inequality, we have:
PQ+PT>QT
Hint: Remember that the sum of any two sides of a triangle must be greater than the third side.
Step 3: Substitute QT with QS+ST
- Since QT is the same as QS+ST, we can rewrite the inequality:
PQ+PT>QS+ST
- Label this as Equation (1).
Hint: This step involves recognizing that QT can be expressed in terms of QS and ST.
Step 4: Apply the Triangle Inequality in triangle RST
- In triangle RST, again by the triangle inequality, we have:
ST+TR>SR
Hint: Use the same reasoning as in Step 2 for this triangle.
Step 5: Substitute ST+TR with SR
- We can rewrite this inequality as:
ST+TR>SR
- Label this as Equation (2).
Hint: Make sure to keep track of which segments belong to which triangle.
Step 6: Combine Equations (1) and (2)
- Now, add the inequalities from Equation (1) and Equation (2):
(PQ+PT)+(ST+TR)>(QS+ST)+SR
- This simplifies to:
PQ+PT+ST+TR>QS+SR
Hint: When adding inequalities, ensure that you combine like terms correctly.
Step 7: Simplify the left side
- Notice that PT+TR is equal to PR:
PQ+PR>QS+SR
Hint: Recognizing equivalent segments is key to simplifying the expression.
Step 8: Rearranging gives the final result
- Rearranging the inequality gives us:
SQ+SR<PQ+PR
Hint: The final step is just a matter of rearranging terms to get the desired inequality.
Conclusion
Thus, we have shown that SQ+SR<PQ+PR as required.
- Draw triangle PQR with point S inside it.
- Extend line QS to meet line PR at point T.
- In triangle PQT, by the triangle inequality, we have:
PQ+PT>QT
Hint: Remember that the sum of any two sides of a triangle must be greater than the third side.
- Since QT is the same as QS+ST, we can rewrite the inequality:
PQ+PT>QS+ST
- Label this as Equation (1).
- In triangle RST, again by the triangle inequality, we have:
ST+TR>SR
Hint: Use the same reasoning as in Step 2 for this triangle.
- We can rewrite this inequality as:
ST+TR>SR
- Label this as Equation (2).
- Now, add the inequalities from Equation (1) and Equation (2):
(PQ+PT)+(ST+TR)>(QS+ST)+SR
- This simplifies to:
PQ+PT+ST+TR>QS+SR
- Notice that PT+TR is equal to PR:
PQ+PR>QS+SR
- Rearranging the inequality gives us:
SQ+SR<PQ+PR
Thus, we have shown that SQ+SR<PQ+PR as required.
Topper's Solved these Questions
Similar Questions
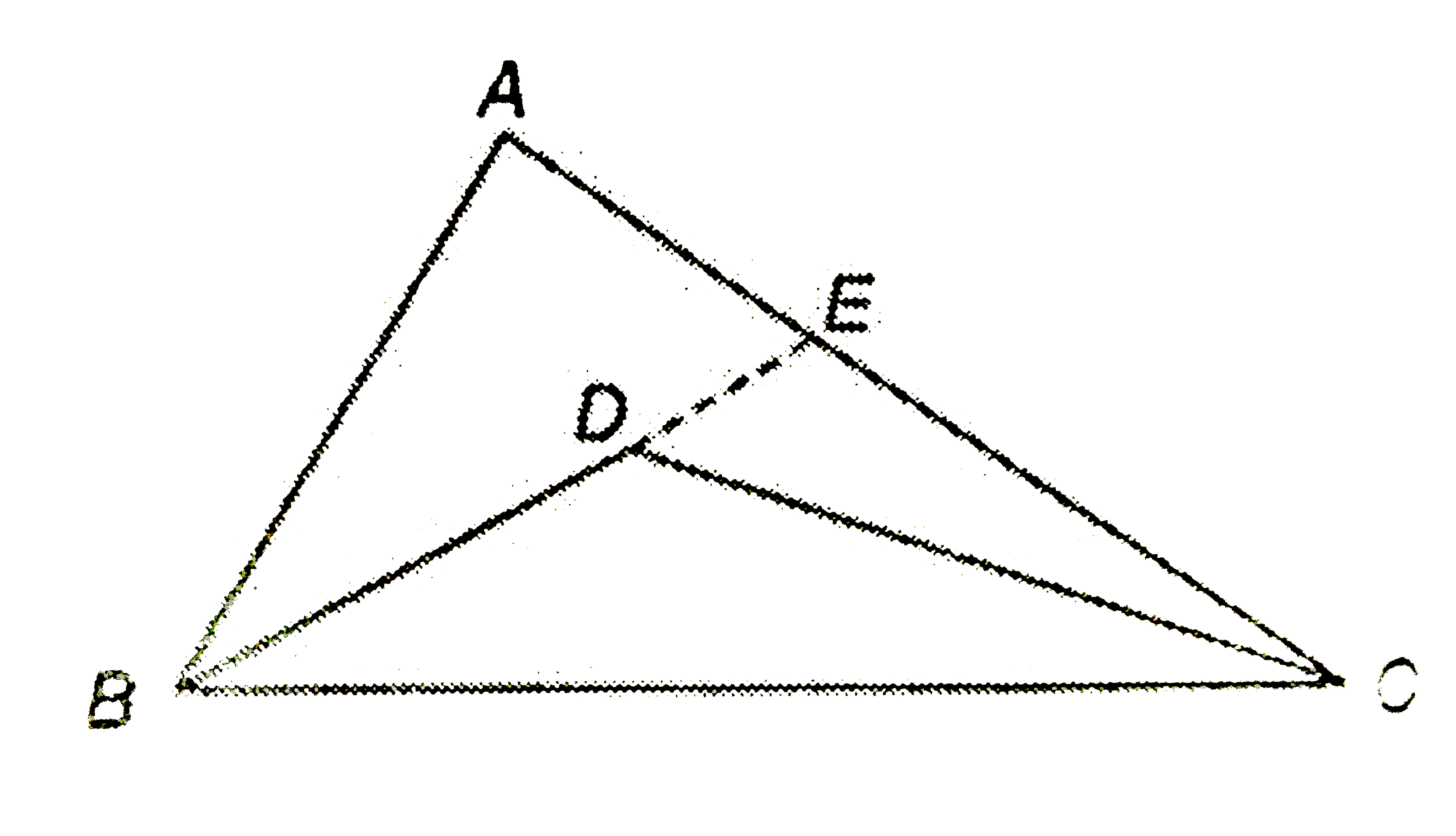
In the adjoining figure, ABC is a triangle and D is any point in its interior. Show that BD+DC<AB+AC.
View SolutionIn Figure, PQRS is a square. Determine ∠SRP.
View SolutionIn Figure, PQRS and ABRS are parallelograms and X is any point on side BR. Show that : ar(∣∣gmPQRS)=ar(∣∣gmABRS), ar(△AXS)=12ar(∣∣gmPQRS)
View SolutionIn Figure, PQRS is a square and SRT is an equilateral triangle. Prove that PT=QT (ii) ∠TQR=150
View SolutionIn Fig. 9.17, PQRS and ABRS are parallelograms and X is any point on side BR. Show that (i) ar(PQRS)=ar(ABRS)(ii) ar(AXS) =12ar(PQRS)
View SolutionIn PQR , S is any point on the side QR . Show that PQ+QR+RP>2PS
View SolutionDraw a rough sketch of a triangle ABC. Mark a point P in its interior and a point Q in its exterior. Is the point A in its exterior or in its interior?
View SolutionPQR is a triangle is which PQ=PR and S is any point on the side PQ . Through S, a line is drawn parallel to QR and intersecting PR at T. Prove that PS=PT
View SolutionPQR is a triangle in which PQ=PR and S is any point on the side PQ . Through S, a line is drawn parallel to QR and intersecting PR at T. Prove that PS=PT.
View SolutionIn Figure, PQRS is a quadrilateral. PQ is its longest side and RS is its shortest side. Prove that ∠R> ∠P and ∠S> ∠Q.
View Solution
